Question

In a convex hexagon, prove that the sum of all the interior angles is equal to twice the sum of its exterior angles formed by producing the sides in the same order.

Answer 1

Hint – In this question use the concept that the sum of interior angles of a n-sided closed polygon is $\left( {n - 2} \right){180^0}$, where n is the number of sides, and the sum of exterior angles of a closed polygon is ${360^0}$. The n is this question is 6.

Complete step by step answer:

Proof –
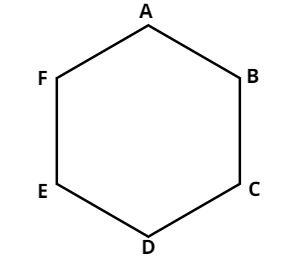
Let us consider the regular convex hexagon ABCDEF.
As we know in a regular hexagon number of sides (n) = 6.
And we also know that in any polygon the sum (Sin) of interior angle is = $\left( {n - 2} \right){180^0}$, where n is the number of sides of the polygon.
$ \Rightarrow {S_{in}} = \left( {n - 2} \right){180^0}$
$ \Rightarrow {S_{in}} = \left( {6 - 2} \right){180^0} = 4\left( {{{180}^0}} \right) = {720^0}$....................... (1)
Now we also know that in any polygon the sum (Sex) angle is always equal to 3600.
$ \Rightarrow {S_{ex}} = {360^0}$..................... (2)
Now from equation (1) and (2) we can say that, sum of interior angles is equal to two times the sum of exterior angles.
${S_{in}} = 2{S_{ex}}$
So the sum of all interior angles in a convex hexagon is equal to twice the sum of its exterior angles.
Hence Proved.

Note – A convex hexagon has no angle pointing inwards. In a convex hexagon no internal angle is greater than${180^0}$, this acts as the main difference between a concave and a convex hexagon as in concave hexagon the interior angle can be greater than${180^0}$.