Question

In a face centred cubic lattice, all atoms at face are shared equally by how many unit cells?
A.8
B.4
C.2
D.6

Answer 1

Hint: In the face centred cubic arrangement, eight atoms are present at the corners of the unit cell and one atom centred in each of the faces. The atom in the face is shared with the adjacent cell.

Complete step-by-step solution:
A unit cell is the smallest repeating portion of a crystal lattice. It has eight corners, twelve edges and six faces. There are three different types of unit cells:
Simple cubic
Face-centred cubic
Body-centred cubic
Particularly in FCC, the eight atoms at the corners contribute \[{\text{8 }} \times {\text{ }}\dfrac{1}{8}{\text{ = 1}}\]. There is one atom at each of the six faces which is shared by two unit cells each. Therefore, the contribution of six face-centred atoms \[6 \times {\text{ }}\dfrac{1}{2}{\text{ = 3}}\]. Total number of atoms be \[1{\text{ + 3 = 4}}\].

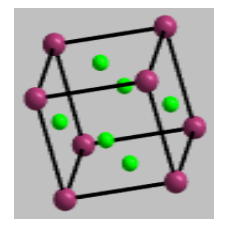
No matter what the crystal lattice be, each unit cell is always connected to six other unit cells and thereby each face of the unit cell is connected to any one face of another unit cell.
Hence, all atoms at face are shared equally by two adjacent unit cells. So, the correct option is (C).

Note: We can think of it in another way such that each face of the cell is common to two adjacent cells. Therefore, the contribution of each face-centred atom is only half of its mass and volume to one cell. Similarly, if we arrange six cells, each will share the remaining half of the face-centred atoms.