Question

In a metre bridge, the balancing length from the left end (standard resistance of one ohm is in the right gap) is found to be \[20{\rm{ cm}}\]. The value of the unknown resistance is
A. \[4{\rm{ }}\Omega \]
B. \[0.5{\rm{ }}\Omega \]
C. \[0.4{\rm{ }}\Omega \]
D. \[0.25{\rm{ }}\Omega \]

Answer 1

Hint: The ratio of resistances on the left end and right end of the given meter bridge will be equal to the ratio of the distance between the left end and right end and jockey. We will use this expression for the metre bridge to calculate the value of unknown resistance.

Complete step by step answer:
Given:
The balancing length from the left end is \[l = 20{\rm{ cm}}\].
The value of resistance in the right gap is \[{R_2} = 1{\rm{ }}\Omega \].

We have to find the value of unknown resistance \[{R_2}\].

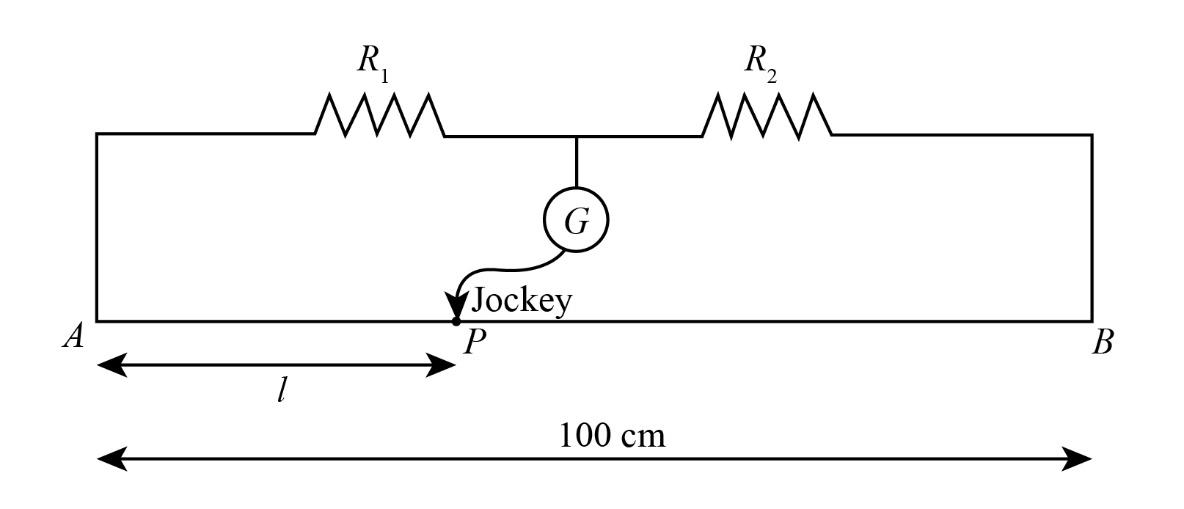
It is given that the metre bridge is in a balanced condition, so the value of the current through the jockey will be zero.

We can write the expression for balanced metre bridge as below:
\[\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{\rm{AP}}}}{{{\rm{BP}}}}\]……(1)

We know that the length of the metre bridge is \[100{\rm{ cm}}\].
\[{\rm{AB}} = 100{\rm{ cm}}\]

Therefore from the above diagram, we can say that the distance between point B and point P is \[\left( {100 - l} \right){\rm{ cm}}\].
\[{\rm{BP}} = \left( {100{\rm{ cm}} - l} \right)\]

Substitute \[l\] for AP and \[\left( {100{\rm{ cm}} - l} \right)\] for BP in equation (1).
\[\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{l}{{\left( {100{\rm{ cm}} - l} \right)}}\]

Substitute \[20{\rm{ cm}}\] for l and \[1{\rm{ }}\Omega \] for \[{R_2}\] in the above expression.
\[\begin{array}{l}
\dfrac{{{R_1}}}{{1{\rm{ }}\Omega }} = \dfrac{{20{\rm{ cm}}}}{{100{\rm{ cm}} - 20{\rm{ cm}}}}\\
{R_1} = 0.25{\rm{ }}\Omega
\end{array}\]

Therefore, the value of unknown resistance is \[0.25{\rm{ }}\Omega \]

So, the correct answer is “Option D”.

Note:
In metre bridge, a wire of length one-metre having uniform cross-sectional area is mounted between two clips of metals which are bent at right angles in such a way that the provision for the introduction of two resistors is provided. A battery is connected to the endpoints of the wire. Also, there is a galvanometer whose one end is connected to the strip and another to a jockey. This jockey is moved across the length of the wire, and unknown resistance is calculated.