Question

In a non-uniform circular motion, the ratio of tangential to radial acceleration is (r=radius of a circle, v=speed of the particle, $\alpha $= angular acceleration.
A. $\dfrac{{{\alpha ^2}{r^2}}}{v} $
B. $\dfrac{{{\alpha ^2}r}}{{{v^2}}} $
C. $\dfrac{{\alpha {r^2}}}{{{v^2}}}$
D. $\dfrac{{{v^2}}}{{{r^2}\alpha }} $

Answer 1

Hint: In non-ideal cases, the circular motion of a body will not have constant angular velocity but it will slow down or pick up pace regularly. The total acceleration of a body moving in a circular motion is the resultant of two types of accelerations, namely Centripetal and Tangential acceleration.
$\overrightarrow a = {\overrightarrow a _c} + {\overrightarrow a _t}$

Complete step by step answer:
Let us consider a non-uniform circular motion as shown below,

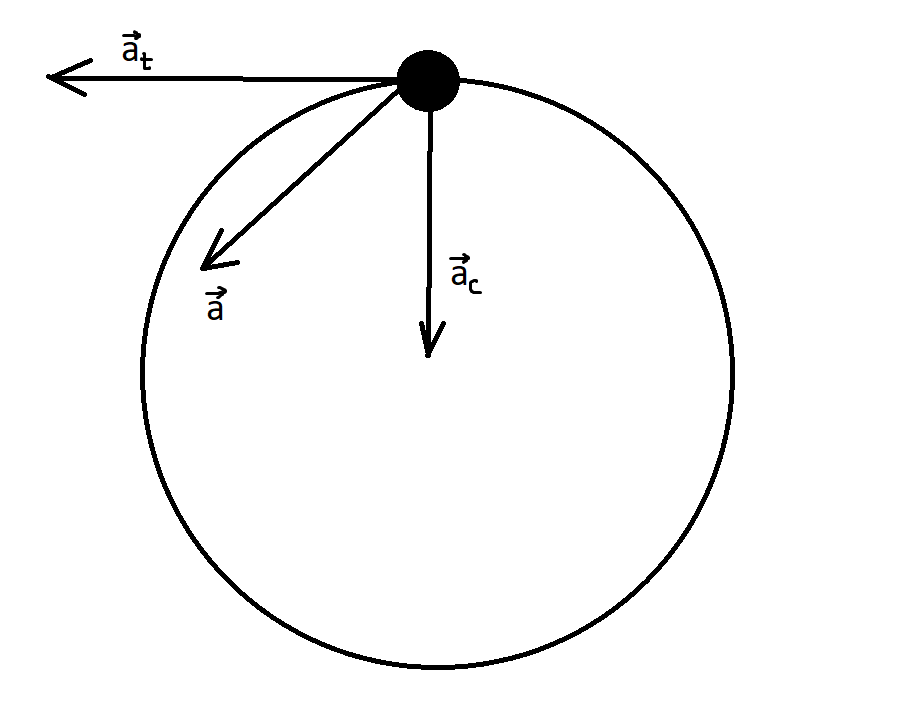
In a non-uniform circular motion, the body not only changes its angular velocity per unit time but also, the direction of the velocity vector. Since the velocity vector, which is a tangent to the direction of motion of the body, keeps changing every second, we get an additional component of acceleration. This component of acceleration is called Tangential acceleration.
Tangential acceleration, $\left| {{a_t}} \right| = r\alpha $
$\alpha $ is called the angular acceleration, which means the change in angular velocity in radians per second.
$\alpha = \dfrac{\omega }{t}$
There is one more component of acceleration, for the actual change in the velocity per unit time and is directed towards the center of the circle. This is called Centripetal acceleration. This is also called Radial acceleration.
Centripetal acceleration, $\left| {{a_c}} \right| = \dfrac{{{v^2}}}{r}$
The ratio of Tangential acceleration to Radial acceleration is,
$\Rightarrow \dfrac{{{a_t}}}{{{a_c}}} = \dfrac{{r\alpha }}{{\dfrac{{{v^2}}}{r}}}$
Simplifying, we get
$\Rightarrow \dfrac{{{a_t}}}{{{a_c}}} = \dfrac{{r\alpha \times r}}{{{v^2}}}$
$\Rightarrow \dfrac{{{a_t}}}{{{a_c}}} = \dfrac{{\alpha {r^2}}}{{{v^2}}} $

Thus, the correct option is Option C.

Note:
Sometimes, you may get confused while marking the directions of components of the acceleration. So, remember this fact.
Tangential acceleration will always be a tangent to the circle. Just like a tangent, it will touch the circle only at one point and will be perpendicular to the radius.
Centripetal acceleration will be directed towards the center because it has the centre of the words in it.