Question

In a parallelogram ABCD, P and Q are the mid – points of BC and CD then the area of the triangle \[\Delta APQ\]will be how many times the area of parallelogram.
(a) \[\dfrac{1}{2}\]
(b) \[\dfrac{1}{4}\]
(c) \[\dfrac{1}{8}\]
(d) \[\dfrac{3}{8}\]

Answer 1

Hint: We solve this problem by drawing a rough figure of given information as follows.

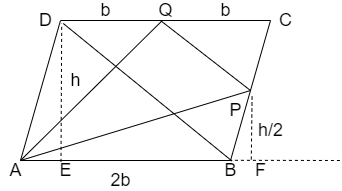
Here we find the areas of all the triangles which are required such that the sum of those areas will equal to area of parallelogram that is
\[\Rightarrow A\left( ABCD \right)=A\left( \Delta APQ \right)+A\left( \Delta ABP \right)+A\left( \Delta ADQ \right)+A\left( \Delta CPQ \right)\]
We find the area of \[\Delta APQ\] to find the ratio of area of \[\Delta APQ\] with the area of parallelogram.
We use the formula of area of triangle and area of parallelogram as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
\[\text{Area of parallelogram}=\left( base \right)\left( height \right)\]

Complete step-by-step answer:
We are asked to find the ratio of area of triangle \[\Delta APQ\] and area of parallelogram ABCD.
We know that by dividing the area of parallelogram we get the sum of areas of divided parts equal to area of parallelogram that is
\[\Rightarrow A\left( ABCD \right)=A\left( \Delta APQ \right)+A\left( \Delta ABP \right)+A\left( \Delta ADQ \right)+A\left( \Delta CPQ \right).......equation(i)\]
Let us assume that the base of parallelogram as \['2b'\] and the height of parallelogram as \['h'\] shown in figure.
We know that the formula for area of parallelogram as
\[\text{Area of parallelogram}=\left( base \right)\left( height \right)\]
By using the above formula we get
\[\begin{align}
  & \Rightarrow A\left( ABCD \right)=\left( 2b \right)\left( h \right) \\
 & \Rightarrow A\left( ABCD \right)=2bh \\
\end{align}\]
Now, let us consider the triangle \[\Delta ABP\]
We are given that point P is the mid – point of BC which lies between the parallel lines.
We know that the mid – point of any line between two parallel lines will be mid – point of all lines drawn between those two parallel lines that is
\[\begin{align}
  & \Rightarrow PF=\dfrac{DE}{2} \\
 & \Rightarrow PF=\dfrac{h}{2} \\
\end{align}\]
We know that the formula for area of triangle as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
By using the above formula we get
\[\begin{align}
  & \Rightarrow A\left( \Delta ABP \right)=\dfrac{1}{2}\left( AB \right)\left( PF \right) \\
 & \Rightarrow A\left( \Delta ABP \right)=\dfrac{1}{2}\left( 2b \right)\left( \dfrac{h}{2} \right) \\
 & \Rightarrow A\left( \Delta ABP \right)=\dfrac{bh}{2} \\
\end{align}\]
Now let us consider the triangle \[\Delta AQD\]
Now, by using the area formula of triangle we get
\[\begin{align}
  & \Rightarrow A\left( \Delta AQD \right)=\dfrac{1}{2}\left( DQ \right)\left( DE \right) \\
 & \Rightarrow A\left( \Delta AQD \right)=\dfrac{1}{2}\left( b \right)\left( h \right) \\
 & \Rightarrow A\left( \Delta AQD \right)=\dfrac{bh}{2} \\
\end{align}\]
Now let us find the area of triangle \[\Delta CPQ\]
Here, we can see that points P, Q are the mid – points of lines BC and CD respectively.
So, we can say that lines PQ and CD are parallel to each other that is
\[\Rightarrow PQ\parallel BC\]
Now, let us consider the triangles \[\Delta CPQ\] and \[\Delta CDB\]

Here, we can write the angles from the two triangles as
\[\begin{align}
  & \Rightarrow \angle PCQ=\angle BCQ\left( \because \text{common angle} \right) \\
 & \Rightarrow \angle CQP=\angle CDB\left( \because PQ\parallel BC \right) \\
 & \Rightarrow \angle CPQ=\angle CBD\left( \because PQ\parallel BC \right) \\
\end{align}\]
Now, from the AAA similarity of two triangles we can say that the triangles \[\Delta CPQ\] and \[\Delta CDB\] are similar that is
\[\Rightarrow \Delta CPQ\sim \Delta CBD\]
We know that when two triangles are similar to each other, then, the ratio of areas of those two similar triangles is equal to square of ratio of their corresponding sides that is
\[\Rightarrow \dfrac{A\left( \Delta CPQ \right)}{A\left( \Delta CBD \right)}={{\left( \dfrac{CQ}{CD} \right)}^{2}}\]
Now, by substituting the required values in above equation we get
\[\begin{align}
  & \Rightarrow A\left( \Delta CPQ \right)={{\left( \dfrac{b}{2b} \right)}^{2}}\left( A\left( \Delta CBD \right) \right) \\
 & \Rightarrow A\left( \Delta CPQ \right)=\dfrac{A\left( \Delta CBD \right)}{4}.....equation(ii) \\
\end{align}\]
Now, by using the area formula of triangle we get the area of \[\Delta CBD\] as
\[\Rightarrow A\left( \Delta CBD \right)=\dfrac{1}{2}\left( 2b \right)\left( h \right)=bh\]
By substituting this value in equation (ii) we get
\[\Rightarrow A\left( \Delta CPQ \right)=\dfrac{bh}{4}\]
Now let us take the equation (i) and by substituting the required areas we get
\[\begin{align}
  & \Rightarrow A\left( ABCD \right)=A\left( \Delta APQ \right)+A\left( \Delta ABP \right)+A\left( \Delta ADQ \right)+A\left( \Delta CPQ \right) \\
 & \Rightarrow 2bh=A\left( \Delta APQ \right)+\dfrac{bh}{2}+\dfrac{bh}{2}+\dfrac{bh}{4} \\
 & \Rightarrow A\left( \Delta APQ \right)=2bh-\left( \dfrac{bh}{2}+\dfrac{bh}{2}+\dfrac{bh}{4} \right) \\
\end{align}\]
Now, by adding the terms using the LCM we get
\[\begin{align}
  & \Rightarrow A\left( \Delta APQ \right)=\dfrac{8bh-2bh-2bh-bh}{4} \\
 & \Rightarrow A\left( \Delta APQ \right)=\dfrac{3}{4}bh \\
\end{align}\]
Now, by dividing the area of \[\Delta APQ\] with the area of parallelogram ABCD we get
\[\begin{align}
  & \Rightarrow \dfrac{A\left( \Delta CPQ \right)}{A\left( ABCD \right)}=\dfrac{\dfrac{3}{4}bh}{2bh} \\
 & \Rightarrow A\left( \Delta CPQ \right)=\dfrac{3}{8}\times A\left( ABCD \right) \\
\end{align}\]
Therefore, we can conclude that the area of the triangle \[\Delta APQ\] is \[\dfrac{3}{8}\] times area of parallelogram.

So, the correct answer is “Option (d)”.

Note: Students may make mistakes in the calculations part because we used many theorems and formulas in this problem.
The formulas and theorems that are used in this problem are
(i) The formula for area of parallelogram as
\[\text{Area of parallelogram}=\left( base \right)\left( height \right)\]
(ii) The formula for area of triangle as
\[\text{Area of triangle}=\dfrac{1}{2}\left( base \right)\left( height \right)\]
(iii) The mid – point of any line between two parallel lines will be mid – point of all lines drawn between those two parallel lines that is
\[\Rightarrow PF=\dfrac{DE}{2}\]
(iv) The ratio of areas of those two similar triangles is equal to square of ratio of their corresponding sides that is
\[\Rightarrow \dfrac{A\left( \Delta CPQ \right)}{A\left( \Delta CBD \right)}={{\left( \dfrac{CQ}{CD} \right)}^{2}}\]
These theorems are standard ones which need to be remembered.