
In a quark model of elementary particles, a neutron is made of one up quark of charge
A. 7.68
B. -5.21
C. -0.48
D. 9.34
Answer
438.9k+ views
Hint: The potential energy of the given equilateral triangular system with 3 charges (the quarks are considered to be as the charges) can be obtained as the algebraic sum of the potential energies of each pair. Here, we get 3 pairs, 1 pair is down quark and down quark and the other 2 pairs are of up quark and down quark.
Complete step by step answer:
From the given information, we have the data as follows.
The total number of up quarks for neutron, 1
The total number of down quarks for neutron, 2
The charge on an up quark,
The charge on a down quark,
The distance between each quark,
The quarks are arranged on the vertices of an equilateral triangle with a side of
Where
Consider the diagram representing the given information.
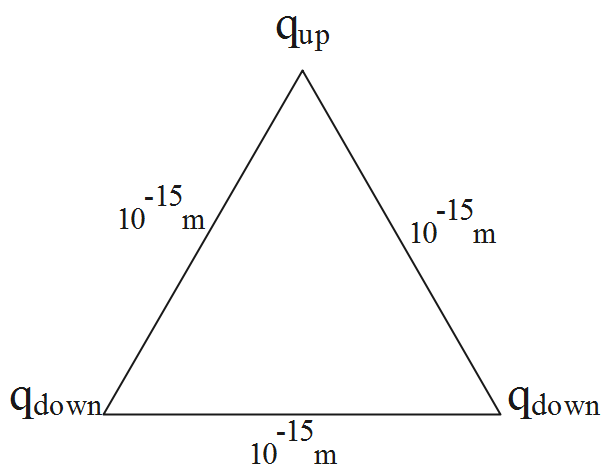
The potential energy of the given equilateral triangular system with 3 charges (the quarks are considered to be as the charges) can be obtained as the algebraic sum of the potential energies of each pair.
The formula representing the same is given as follows.
Substitute the values in the above formula.
Continue further computation.
The potential energy in terms of the Joules is
In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on the electron, so, we have,
Thus, the value of the potential energy in terms of MeV is,
So, the correct answer is “Option C”.
Note: The quarks are considered to be charges, as they carry some energy. In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on an electron. This conversion method should be known to get the final answer.
Complete step by step answer:
From the given information, we have the data as follows.
The total number of up quarks for neutron, 1
The total number of down quarks for neutron, 2
The charge on an up quark,
The charge on a down quark,
The distance between each quark,
The quarks are arranged on the vertices of an equilateral triangle with a side of
Where
Consider the diagram representing the given information.

The potential energy of the given equilateral triangular system with 3 charges (the quarks are considered to be as the charges) can be obtained as the algebraic sum of the potential energies of each pair.
The formula representing the same is given as follows.
Substitute the values in the above formula.
Continue further computation.
The potential energy in terms of the Joules is
In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on the electron, so, we have,
Thus, the value of the potential energy in terms of MeV is,
So, the correct answer is “Option C”.
Note: The quarks are considered to be charges, as they carry some energy. In order to convert the potential energy from Joules into the eV, we have to divide the value of the energy by the charge on an electron. This conversion method should be known to get the final answer.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

Draw a diagram of a flower and name the parts class 12 biology ICSE




