Question

In a rectangle, the difference between the sum of adjacent sides and the diagonal is half the length of the longer side. What is the ratio of the shorter to the longer side?
A. $\sqrt 3 :2$
B. $1:\sqrt 3 $
C. $2:5$
D. $3:4$

Answer 1

Hint: To solve this problem we have to know about some properties of a rectangle. A rectangle is a four-sided closed polygon. The opposite sides of a rectangle are parallel and equal. The adjacent sides of the rectangle are always perpendicular to each other. In a rectangle one side is shorter while its adjacent side is longer.

Complete step by step answer:
Consider a rectangle, the diagonal of a rectangle divides the rectangle into two equal right angle triangles, hence the right angled triangle obeys the Pythagoras theorem.

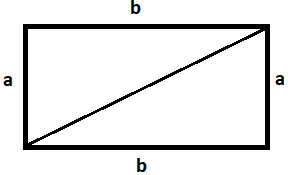
Let the length of the longer side of the rectangle be $'b'$
The length of the short side of the rectangle be $'a'$
As the right angled triangle obeys the Pythagoras theorem, hence the length of the diagonal can be obtained.
The length of the diagonal of the rectangle is $\sqrt {{a^2} + {b^2}} $.
The sum of the adjacent sides of the rectangle = $a + b$
Given that the difference between the sum of adjacent sides and the diagonal is half the length of longer side, is given below:
$ \Rightarrow (a + b) - \sqrt {{a^2} + {b^2}} = \dfrac{1}{2}b$
$ \Rightarrow a + b - \dfrac{b}{2} = \sqrt {{a^2} + {b^2}} $
$ \Rightarrow a + \dfrac{b}{2} = \sqrt {{a^2} + {b^2}} $
Squaring on both sides, as given below:
\[ \Rightarrow {\left( {a + \dfrac{b}{2}} \right)^2} = {\left( {\sqrt {{a^2} + {b^2}} } \right)^2}\]
\[ \Rightarrow {a^2} + \dfrac{{{b^2}}}{4} + 2\dfrac{{ab}}{2} = {a^2} + {b^2}\]
\[ \Rightarrow ab = \dfrac{{3{b^2}}}{4}\]
Dividing the above expression by $b$on both sides, as given below :
\[ \Rightarrow a = \dfrac{{3b}}{4}\]
\[ \Rightarrow \dfrac{a}{b} = \dfrac{3}{4}\]

The ratio of the shorter to the longer side is 3:4.

Note: Please note that all rectangles are squares but all squares are not rectangles. In a square all sides should be equal, while the opposite sides should be parallel and adjacent sides should be perpendicular to each other. Whereas in a rectangle all sides need not be equal, the opposite sides should be equal and parallel, while the adjacent sides should be perpendicular to each other. Here if in a rectangle if the adjacent sides are equal then it is a square.