Question

In a regular hexagonal prism, the longest diagonal is 12 ft. Find the volume of the prism if the diagonal makes an angle of 30 degrees with a lateral edge.

Answer 1

Hint: To solve the above question, we will have to find the base area and the height of the prism for calculating the volume of the prism. Now, we do not know the area of the prism base. For this, we will first find the side of the regular hexagon. For finding the side, we will apply Pythagoras theorem in the right-angled triangle formed due to the prism diagonal, base diagonal, and lateral edge. We will get another equation by applying trigonometric ratio in this triangle. From these two equations, we will get the length of the lateral side (height) and the base diagonal. Now, the side will be half of the base diagonal. After finding the side of the hexagon, we will find the base area and multiply it with the height to get the volume.
Complete step by step solution:
It is given that the longest diagonal is 12 feet. The longest diagonal will be formed when the vertex of one base will be joined to the opposite vertex of the other base. Let us assume that the length of each side of the hexagonal base is x. Now the lateral edge will be equal to the height. Let the height be h. Now, we will see the figure of the regular hexagonal prism for a better understanding.

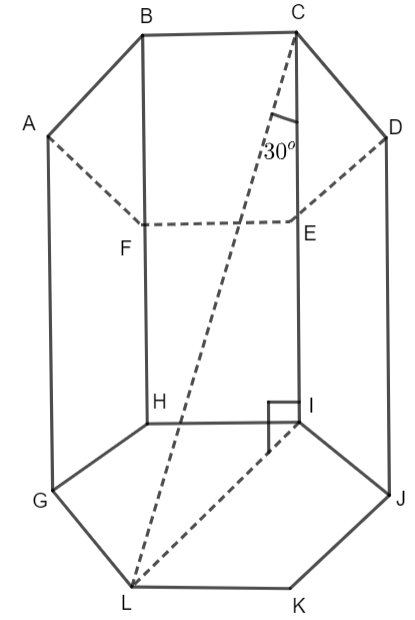
We can see from the above figure that ABCDEF and GHIJKL are regular hexagonal bases having each side x. LC is the longest diagonal of the prism and LI is the base diagonal. The triangle CLI is a right-angled and the angle between the diagonal CL and the height CI is \[{{30}^{o}}.\]
We are going to use a property of a regular hexagon which says that the length of the longest diagonal is twice the side. Thus, we will get,
\[LI=2x.....\left( i \right)\]
Now, we will use the Pythagoras theorem in triangle CLI. According to Pythagoras theorem, if H is the hypotenuse, B is the base and P is the perpendicular, then,
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]
where H = LC, P = CI and B = LI. Thus,
\[{{\left( LC \right)}^{2}}={{\left( CI \right)}^{2}}+{{\left( LI \right)}^{2}}\]
\[\Rightarrow {{\left( 12 \right)}^{2}}={{h}^{2}}+{{\left( 2x \right)}^{2}}\left[ \text{From (i)} \right]\]
\[\Rightarrow 144={{h}^{2}}+4{{x}^{2}}\]
\[\Rightarrow {{h}^{2}}+4{{x}^{2}}=144\]
\[\Rightarrow 4{{x}^{2}}=144-{{h}^{2}}\]
\[\Rightarrow {{x}^{2}}=\dfrac{144-{{h}^{2}}}{4}......\left( ii \right)\]
Now, it is given that the angle between the height and the diagonal is \[{{30}^{o}}.\] From triangle CLI, we have,

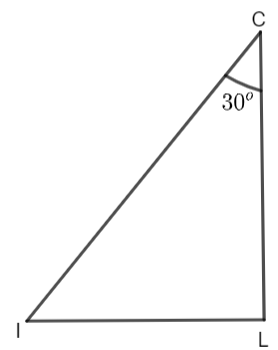
\[\cos {{30}^{o}}=\dfrac{CL}{CI}\]
\[\Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{h}{12}\]
\[\Rightarrow h=6\sqrt{3}feet.....\left( iii \right)\]
From (iii), we will put the value of h in (ii). Thus, we will get,
\[\Rightarrow {{x}^{2}}=\dfrac{144-{{\left( 6\sqrt{3} \right)}^{2}}}{4}\]
\[\Rightarrow {{x}^{2}}=\dfrac{144-108}{4}\]
\[\Rightarrow {{x}^{2}}=\dfrac{36}{4}\]
\[\Rightarrow {{x}^{2}}=9\]
\[\Rightarrow {{x}^{2}}=3feet......\left( iv \right)\]
Thus, the side of the regular hexagon is 3 feet and base diagonal (LI) = 2(3 feet) = 6 feet.
Now, we will consider the hexagon ABCDEF. Thus, we have,

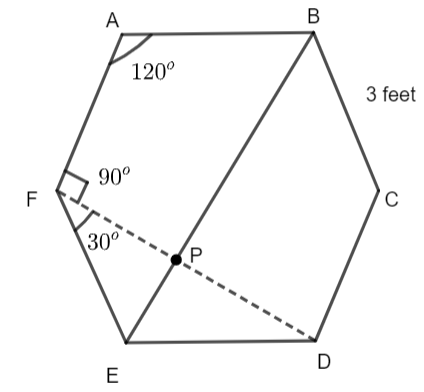
Now, each interior angle in the regular hexagon is \[{{120}^{o}}.\] So, \[\angle FEP={{30}^{o}}.\]
In triangle FEP,
\[\cos {{30}^{o}}=\dfrac{FP}{FE}\]
\[\Rightarrow \dfrac{\sqrt{3}}{2}=\dfrac{FP}{3}\]
\[\Rightarrow FP=\dfrac{3\sqrt{3}}{2}\]
Now, the area of the base of the hexagon will be equal to twice the area of trapezium ABEF. Thus, we have,
Area of ABCDEF = 2 \[\times \] Area of trapezium ABEF.
\[\Rightarrow \text{Area of ABCDEF}=2\times \dfrac{1}{2}\times \left( \text{sum of parallel sides} \right)\times \text{ height}\]
\[\Rightarrow \text{Area of ABCDEF}=\text{sum of parallel sides}\times \text{ height}\]
\[\Rightarrow \text{Area of ABCDEF}=\left( AF+BE \right)\times FP\]
\[\Rightarrow \text{Area of ABCDEF}=\left( 6+3 \right)\times \dfrac{3\sqrt{3}}{2}\]
\[\Rightarrow \text{Area of ABCDEF}=\dfrac{27\sqrt{3}}{2}\text{ square feet}\]
Now, the volume of the prism obtained by multiplying the area of the base by the height
The volume of prism = Base area \[\times \] height
\[\Rightarrow \text{Volume of prism}=\left( \dfrac{27\sqrt{3}}{2}\text{square feet} \right)\times 6\sqrt{3}\text{ feet}\]
\[\Rightarrow \text{Volume of prism}=\dfrac{27\times 3\times 6}{2}\text{ cubic feet}\]
\[\Rightarrow \text{Volume of prism}=243\text{ cubic feet}\]

Note: The base of the prism which is regular hexagon can be calculated by another method which is shown below

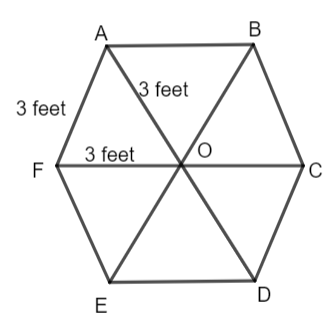
The area of ABCDEF will be 6 times the area of the equilateral triangle AFO. Thus, we have,
\[\Rightarrow \text{Area of ABCDEF}=6\times \dfrac{\sqrt{3}}{4}{{a}^{2}}\]
\[\Rightarrow \text{Area of ABCDEF}=6\times \dfrac{\sqrt{3}}{4}\times {{3}^{2}}\text{ square feet}\]
\[\Rightarrow \text{Area of ABCDEF}=\dfrac{6\times \sqrt{3}\times 9}{4}\text{ square feet}\]
\[\Rightarrow \text{Area of ABCDEF}=\dfrac{27\sqrt{3}}{2}\text{ square feet}\]