Question

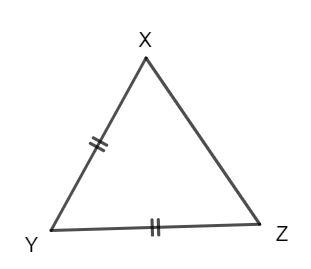
In a triangle XYZ, XY = YZ, then which of the following is true?

(a). \[\angle X = \angle Y\]
(b). \[\angle Y = \angle Z\]
(c). \[\angle Z = \angle X\]
(d). \[\angle X = \angle Y = \angle Z\]

Answer 1

Hint: Recall the properties of a triangle and the different types of triangles and then properties of angles opposite to equal sides, that is the angles opposite to equal sides are also equal.

Complete step-by-step answer:
A triangle is a three-sided polygon with three angles subtended between the three sides.
Special kinds of triangles include the isosceles triangle, right-angle triangle, and equilateral triangle.
A scalene triangle is a triangle with all sides of differing sizes.
An isosceles triangle is a triangle with any two sides equal.
In our given problem, it is given that XY = YZ, the two sides are equal, hence the triangle XYZ is an isosceles triangle.
For an isosceles triangle, the angles opposite to the equal sides are equal.
Let us prove the statement. Construct a median YP from the vertex Y of the triangle.

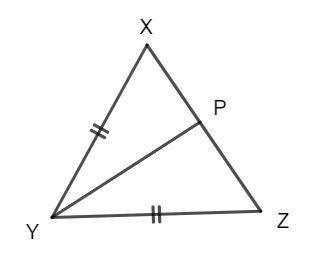
Consider the triangles XYP and ZYP, P is the midpoint of XZ, and hence, we have:
\[XY = YZ\]
\[XP = ZP\]
\[YP = YP\]
Hence, the triangles XYP and ZYP are congruent to each other by SSS (Side-Side-Side) criterion.
\[\Delta XYP \cong \Delta ZYP\]
The corresponding angles of congruent triangles are equal, then, we have:
\[\angle Z = \angle X\]
Hence, the correct answer is option (c).

Note: From the figure, all three sides look equal, so you may conclude wrongly that it is an equilateral triangle and choose option (d) but focus only on given details which is XY = YZ and proceed to solve.