
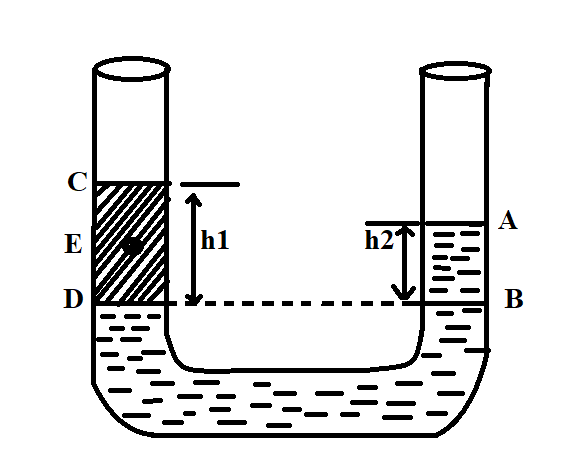
In a U-tube experiment, a column AB of water is balanced by a column CD of paraffin. The relative density of paraffin is:
A) $\dfrac{{{h_2}}}{{{h_1}}}$
B) $\dfrac{{{h_1}}}{{{h_2}}}$
C) $\dfrac{{{h_2} - {h_1}}}{{{h_2}}}$
D) $\dfrac{{{h_2}}}{{{h_1} + {h_2}}}$
Answer
123.6k+ views
Hint: Using Pascal’s law we get that, at the same horizontal level both fluids have the same pressure, i.e. pressure at B and pressure at D will be the same. In a confined incompressible liquid, the changes in pressure will be transmitted throughout the fluid. The pressure is directly proportional to the height and density of the fluid.
Formula used:
$P = {P_0} + h\rho g$ (where $P$ is the pressure due to the liquid, $h$ stands for the height of the liquid, $\rho $stands for the density of the liquid, and $g$ is the acceleration due to gravity)
Complete step by step solution:
According to Pascal’s law, the pressure due to two liquids at the same level will be equal. Thus we can equate the pressure due to both liquids on either side.
On the left side, the pressure is exerted by paraffin and on the right side, the pressure is exerted by water. By using Pascal’s law we can equate both.
$\therefore $Pressure at B= pressure at D
The total pressure at a point is given by the formula,
$P = {P_0} + h\rho g$…………………….
For Paraffin, the height and the density can be written as,
$h = {h_1} $
$ \rho = {\rho _p} $
For water, the height and the density can be written as,
$h = {h_2} $
$\rho = {\rho _w} $
Substituting the above values in equation (1)
${P_0} + {h_1}{\rho _p}g = {P_0} + {h_2}{\rho _w}g$
${h_1}{\rho _p} = {h_2}{\rho _w}$
Taking the ratio of densities, we get
$\dfrac{{{\rho _p}}}{{{\rho _w}}} = \dfrac{{{h_2}}}{{{h_1}}}$
Thus we can write the relative density as,
${\rho _r} = \dfrac{{{h_2}}}{{{h_1}}}$
The correct answer is option (A), $\dfrac{{{h_2}}}{{{h_1}}}.$
Note: The pressure is always acting normal to the area whatever maybe the orientation of the area. The pressure at a depth in a liquid is greater than the atmospheric pressure by an amount$h\rho g$, if the liquid is open to an atmosphere. The excess pressure at a depth h is called the gauge pressure at that point.
Formula used:
$P = {P_0} + h\rho g$ (where $P$ is the pressure due to the liquid, $h$ stands for the height of the liquid, $\rho $stands for the density of the liquid, and $g$ is the acceleration due to gravity)
Complete step by step solution:
According to Pascal’s law, the pressure due to two liquids at the same level will be equal. Thus we can equate the pressure due to both liquids on either side.
On the left side, the pressure is exerted by paraffin and on the right side, the pressure is exerted by water. By using Pascal’s law we can equate both.
$\therefore $Pressure at B= pressure at D
The total pressure at a point is given by the formula,
$P = {P_0} + h\rho g$…………………….
For Paraffin, the height and the density can be written as,
$h = {h_1} $
$ \rho = {\rho _p} $
For water, the height and the density can be written as,
$h = {h_2} $
$\rho = {\rho _w} $
Substituting the above values in equation (1)
${P_0} + {h_1}{\rho _p}g = {P_0} + {h_2}{\rho _w}g$
${h_1}{\rho _p} = {h_2}{\rho _w}$
Taking the ratio of densities, we get
$\dfrac{{{\rho _p}}}{{{\rho _w}}} = \dfrac{{{h_2}}}{{{h_1}}}$
Thus we can write the relative density as,
${\rho _r} = \dfrac{{{h_2}}}{{{h_1}}}$
The correct answer is option (A), $\dfrac{{{h_2}}}{{{h_1}}}.$
Note: The pressure is always acting normal to the area whatever maybe the orientation of the area. The pressure at a depth in a liquid is greater than the atmospheric pressure by an amount$h\rho g$, if the liquid is open to an atmosphere. The excess pressure at a depth h is called the gauge pressure at that point.
Recently Updated Pages
Difference Between Circuit Switching and Packet Switching

Difference Between Mass and Weight

JEE Main Participating Colleges 2024 - A Complete List of Top Colleges

JEE Main Maths Paper Pattern 2025 – Marking, Sections & Tips

Sign up for JEE Main 2025 Live Classes - Vedantu

JEE Main 2025 Helpline Numbers - Center Contact, Phone Number, Address

Trending doubts
JEE Main 2025 Session 2: Application Form (Out), Exam Dates (Released), Eligibility & More

Class 11 JEE Main Physics Mock Test 2025

JEE Main Exam Marking Scheme: Detailed Breakdown of Marks and Negative Marking

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Keys & Solutions

Learn About Angle Of Deviation In Prism: JEE Main Physics 2025

JEE Main 2025: Conversion of Galvanometer Into Ammeter And Voltmeter in Physics

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

NCERT Solutions for Class 11 Physics Chapter 1 Units and Measurements

NCERT Solutions for Class 11 Physics Chapter 9 Mechanical Properties of Fluids

Units and Measurements Class 11 Notes: CBSE Physics Chapter 1

JEE Advanced 2025: Dates, Registration, Syllabus, Eligibility Criteria and More

NCERT Solutions for Class 11 Physics Chapter 2 Motion In A Straight Line




