Question

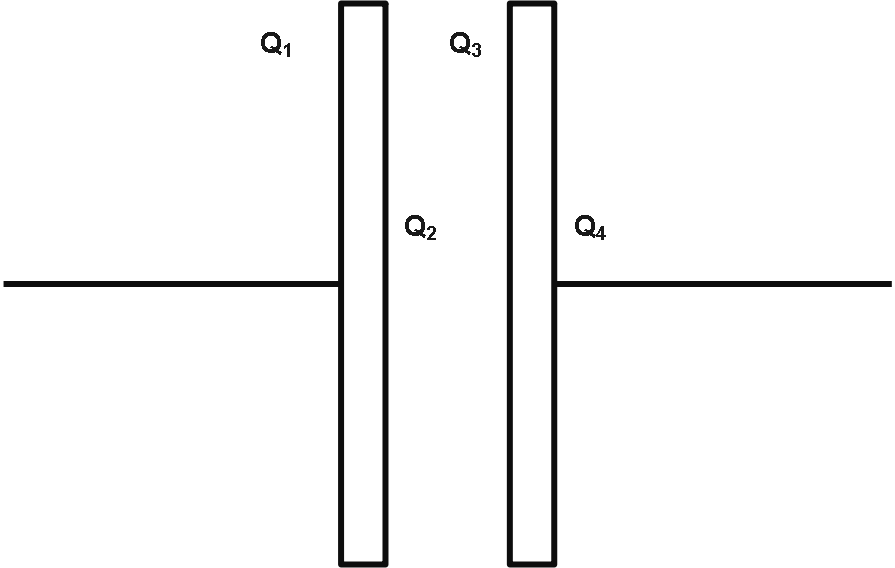
In an isolated parallel plate capacitor of capacitance $C$ , the four surfaces have charges ${Q_1},{Q_2},{Q_3}$ and ${Q_4}$ as shown. The potential difference between the plates is:

(a). $\dfrac{{{Q_1} + {Q_2} + {Q_3} + {Q_4}}}{{2C}}$
(b). $\dfrac{{{Q_2} + {Q_3}}}{{2C}}$
(c). $\dfrac{{{Q_2} - {Q_3}}}{{2C}}$
(d). $\dfrac{{{Q_1} + {Q_4}}}{{2C}}$

Answer 1

Hint: In order to solve this question, one must know about parallel plate capacitors. Here we have used the property that Facing surfaces have equal and opposite charges and then put the values in formula and then added both the equations to get the potential difference.

Formula used:
$Q = CV$
Where,
$Q$ is the charge,
$C$ is the capacitance and
$V$ is the voltage.

Complete answer:
As we know that the charge on a capacitor means the charge on the inner surface of the positive plate.
We also know that,
Facing surfaces have equal and opposite charges.
i.e., ${Q_3} = - {Q_2}$
And we know that the potential difference between the plates is equal to the charge on the capacitor divided by capacitance.
$\therefore V = \dfrac{{{Q_2}}}{C}$ -----(1)
Also, we can write
$\therefore V = \dfrac{{ - {Q_3}}}{C}$ -----(2) because ${Q_3} = - {Q_2}$ .
Now let’s add both the equation,
$
  2V = \dfrac{{{Q_2} - {Q_3}}}{C} \\
   \Rightarrow V = \dfrac{{{Q_2} - {Q_3}}}{{2C}} \\
 $
So, the potential difference between the plates is $V = \dfrac{{{Q_2} - {Q_3}}}{{2C}}$ .
Hence, the correct option is (c).

Note:
Here we have to take care that if the charge is negative, we will not put the negative sign while calculating the potential difference. Also, there would be two electric fields for the two plates of the capacitor.