Question

In an isosceles triangle, the vertex angle is $ {50^ \circ } $ .What are the base angles of the triangle?

Answer 1

Hint: In an isosceles triangle two sides are equal along with two angles. The sum of all the angles of a triangle is $ {180^ \circ } $ so we will use this fact and try to find the measure of base angles using the vertex angle and the property of the sum of angles of a triangle. Here we will get an equation in one variable which can be solved easily to find the unknown variable.

Complete step-by-step answer:
Let $ ABC $ be an isosceles triangle where $ AC = AB $

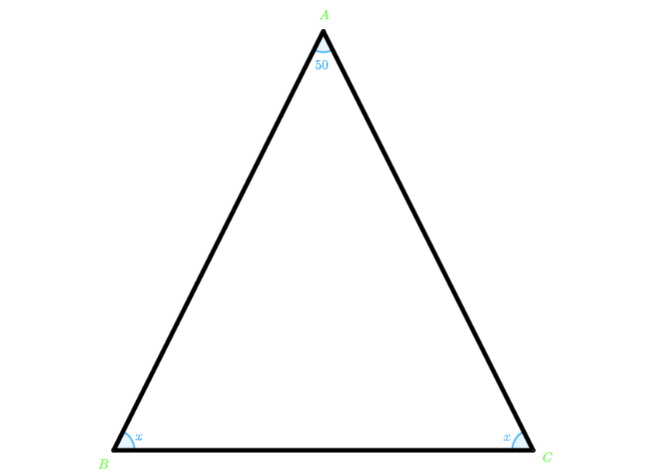
We are given in the question that the measure of vertex angle is $ {50^ \circ } $ , which is $ \angle CAB $
So, $ \angle CAB = {50^ \circ } $
The sum of angles of a triangle is $ {180^ \circ } $
Since the given triangle is an isosceles triangle the angles adjacent to the equal sides ( $ AC $ and $ AB $ ) have also equal magnitude.
We don’t know the measure of these angles, and we are asked to find out their value.
Let us take these two equal angles to be $ x $ .
So,
 $ \angle ACB = \angle ABC = x $
Now we will use the fact that the sum of sides of a triangle is $ {180^ \circ } $ .
So,
\[x + x + {50^ \circ } = {180^ \circ }\]
\[ \Rightarrow 2x + {50^ \circ } = {180^ \circ }\;\;\]
Now we will take $ {50^ \circ } $ to other side of the equation and we get:
\[2x = {180^ \circ } - {50^ \circ }\]
\[ \Rightarrow 2x = {130^ \circ }\]
\[x = {65^ \circ }\]
We assumed that $ \angle ACB = \angle ABC = x $ so putting the value we got in place of \[x\] we get,
 $ \angle ACB = \angle ABC = {65^ \circ } $
Therefore, the base angles of the isosceles triangle whose vertex angle $ {180^ \circ } $ is $ {65^ \circ } $ .

Note: Since, we were asked to find the measure of base angles, we should always prefer to take variables to identify the unknown things.Like in this case we treated the unknown angles to be a variable $ x $ which gave as an equation to solve from which we obtained our final answer.