
In an
A)
B)
C)
D)
Answer
490.8k+ views
1 likes
Hint: In
Complete step by step solution:
According to the question, a
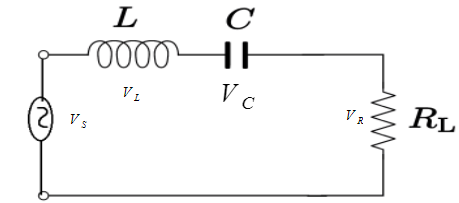
We know that in an
So, the voltage across the
To understand the phase difference in different voltages, we can make a graph which shows the phase difference between voltages.
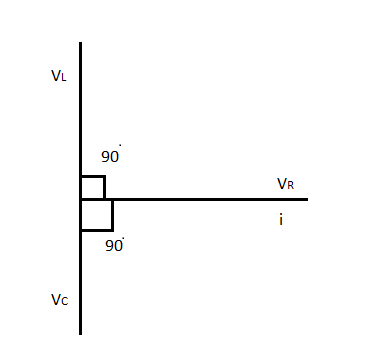
According to the above graph,
Hence, option (D) is correct.
Note: Voltage across the inductor
Complete step by step solution:
According to the question, a
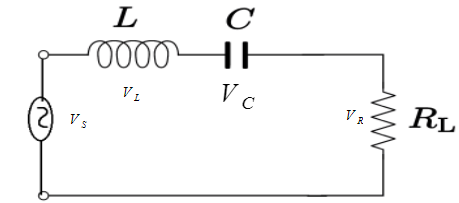
We know that in an
So, the voltage across the
To understand the phase difference in different voltages, we can make a graph which shows the phase difference between voltages.

According to the above graph,
Hence, option (D) is correct.
Note: Voltage across the inductor
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




