Question

In case of a closed organ pipe which harmonic is the ${{P}^{th}}$ overtone will be
A. $2P+1$
B. $2P-1$
C. $P+1$
D. $P-1$

Answer 1

Hint: Study how a closed organ pipe works and what are the types of organ pipes. Learn about the harmonics and overtones and about what they are. Try to define the relation between the harmonics and overtone.

Complete answer:
We have a closed organ pipe. Organ pipes are musical instruments which produce musical sounds by flowing air into the pipe.
We have two types of organ pipes. One is a closed organ pipe and the other is an open organ pipe.
Open organ pipes are open at both ends.

Closed organ pipes are closed at one end. When they are blown at one end the fundamental frequency is produced. If we blow the organ pipe strongly frequencies higher than the fundamental frequency are produced. These are called overtones.

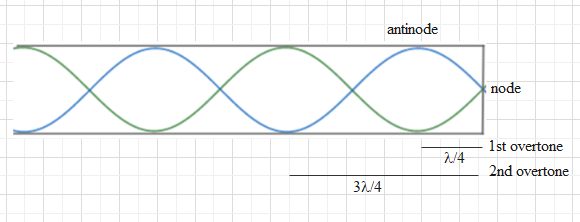
Let the fundamental frequency of the closed organ pipe is $f$.
Then the first overtone will be at $3f$
The second overtone will be $5f$
So, we can say that for nth overtone will be at $2n+1$
Or the harmonics of a overtone can be found out as,
$\text{harmonic = (2}\times \text{overtone)+1}$
We need to find out the harmonic of the Pth overtone of the closed organ pipe.
The harmonic for Pth overtone will be = $2P+1$

So, the correct answer is “Option A”.

Note:
In a closed organ pipe, only the odd harmonics are produced. The frequency of the harmonics in a closed organ pipe are in the ratio $1:3:5.....$

In an open organ pipe we get both the odd and even harmonics. Here the frequency of the harmonics produced are in the ratio $1:2:3....$