Question

In $\Delta MNK$, if $\angle N={{90}^{\circ }}$, $\angle M={{60}^{\circ }}$ and $MN=6$. Then find the value of $NK$?
(a) 6 units
(b) $6\sqrt{3}$ units
(c) $2\sqrt{3}$ units
(d) $5\sqrt{3}$ units

Answer 1

Hint: We start solving the problem by drawing the figure to represent the given information. We then find the hypotenuse by recalling its definition as the side opposite to the right angle. We then recall the definition of tangent of an angle in a right-angled triangle as the ratio of opposite side to the adjacent side. We use this definition for the tangent of the angle $\angle M$ and make necessary calculations to find the required value of $NK$.

Complete step by step answer:
According to the problem, we are given that in $\Delta MNK$ $\angle N={{90}^{\circ }}$, $\angle M={{60}^{\circ }}$ and $MN=6$. We need to find the value of $NK$.
Let us draw the figure representing the given information.

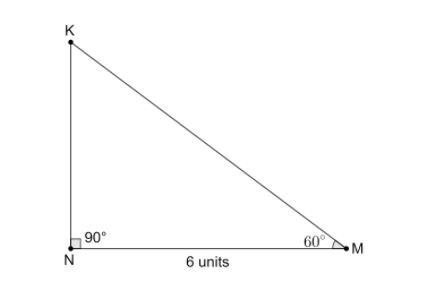
We know that the side opposite to the right angle in a right-angled triangle is hypotenuse which is the largest side of the triangle so, the side MK is the hypotenuse of the side.
We know that the tangent of an angle in a right-angled triangle is defined as the ratio of opposite side to the adjacent side.
So, we get $\tan {{60}^{\circ }}=\dfrac{NK}{MN}$.
$\Rightarrow \sqrt{3}=\dfrac{NK}{6}$.
\[\Rightarrow NK=6\sqrt{3}\] units.
So, we have found the value of NK as \[6\sqrt{3}\] units.

So, the correct answer is “Option b”.

Note: Whenever we get this type of problem, we first try to draw the figure representing the given information as we can see that the figure gave us the better view of the problem. We can also find the length of the hypotenuse by using cosine of the angle $\angle M$ or by using the Pythagoras theorem. We should not confuse $\tan {{60}^{\circ }}$ with $\dfrac{1}{\sqrt{3}}$ instead of $\sqrt{3}$ while solving this problem. Similarly, we can expect problems to find the area of the given triangle.