Question

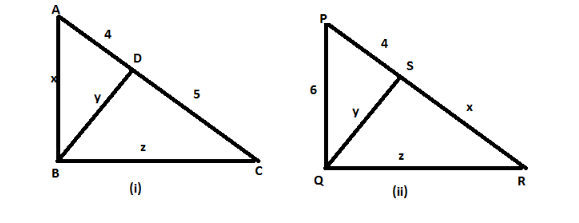
In each figure given below, altitude is drawn on hypotenuse by a right angled triangle. The length of different segments is marked in each figure. Determine x, y, z in each case.

Answer 1

Hint: In both cases there is a right angled triangle (Third side is an altitude) in a right angled triangle.
We can use Pythagora's theorem to establish a relation between inner triangle and outer triangle. Then by using substitution we can find x, y, z.

Complete step-by-step answer:
i.In the given figure,

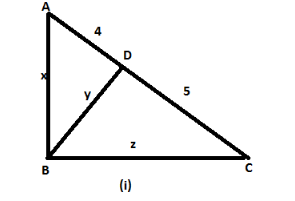
In triangle DBE by Pythagoras theorem,
(In a right triangle square of hypotenuse is equal to the sum of square of height and square of base.)

 $ \begin{align}
  & {{z}^{2}}={{y}^{2}}+{{5}^{2}} \\
 & {{z}^{2}}={{y}^{2}}+25 \\
\end{align} $
                                       ………………….(1)

Now use Pythagoras theorem in triangle ABC
 $ \begin{align}
  & {{(4+5)}^{2}}={{x}^{2}}+{{z}^{2}} \\
 & 81={{x}^{2}}+{{z}^{2}} \\
 & {{z}^{2}}=81-{{x}^{2}} \\
\end{align} $ ………………………….(2)
From equation 1 and 2 we can conclude that,
 $ \begin{align}
  & {{y}^{2}}+25=81-{{x}^{2}} \\
 & {{x}^{2}}+{{y}^{2}}=81-25 \\
 & {{x}^{2}}+{{y}^{2}}=56 \\
\end{align} $ …………………..(3)
Now, in triangle ADB use Pythagoras theorem,
 $ \begin{align}
  & {{x}^{2}}={{y}^{2}}+16 \\
 & {{x}^{2}}-{{y}^{2}}=16 \\
\end{align} $ …………………….. (4)
Now add equation 3 and 4,
 $ \begin{align}
  & {{x}^{2}}+{{y}^{2}}+{{x}^{2}}-{{y}^{2}}=56+16 \\
 & 2{{x}^{2}}=72 \\
 & {{x}^{2}}=36 \\
 & x=6 \\
\end{align} $
We will ignore -6 because the side of a triangle cannot be negative.
Now, put the value of x in equation 3,
 $ \begin{align}
  & {{6}^{2}}+{{y}^{2}}=56 \\
 & {{y}^{2}}=56-36 \\
 & {{y}^{2}}=20 \\
 & y=2\sqrt{5} \\
\end{align} $
Ignore negative values for the same reason.
Again put the value of x in equation 2,
 $ \begin{align}
  & {{z}^{2}}=81-{{6}^{2}} \\
 & {{z}^{2}}=81-36 \\
 & {{z}^{2}}=45 \\
 & z=3\sqrt{5} \\
\end{align} $

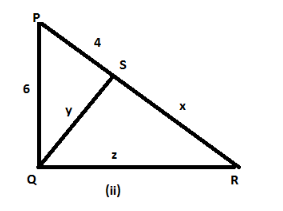
In triangle PSQ, use Pythagoras theorem,
 $ \begin{align}
  & {{6}^{2}}={{4}^{2}}+{{y}^{2}} \\
 & 36-16={{y}^{2}} \\
 & {{y}^{2}}=20 \\
 & y=4\sqrt{5} \\
\end{align} $ ………………….(1)
Use Pythagoras theorem in triangle QSR,
 $ \begin{align}
  & {{z}^{2}}={{x}^{2}}+{{y}^{2}} \\
 & {{z}^{2}}-{{x}^{2}}=20 \\
\end{align} $ (from equation 1) …………………….. (2)
Now, take triangle PQR and apply Pythagoras theorem in it.
 $ {{6}^{2}}+{{z}^{2}}={{(x+4)}^{2}} $
From equation 2 put the value of z in it.
 $ \begin{align}
  & {{6}^{2}}+{{x}^{2}}+20={{x}^{2}}+16+8x \\
 & 56=16+8x \\
 & 8x=40 \\
 & x=5 \\
 & \\
\end{align} $
Put the value of x in equation 2.
 $ \begin{align}
  & {{z}^{2}}-{{5}^{2}}=20 \\
 & {{z}^{2}}=45 \\
 & z=3\sqrt{5} \\
\end{align} $

Note:In figure (i) angle D is a right angle that’s why AB and BC is hypotenuse for triangle ADB and BDC respectively. Same for figure (ii) angle S is a right angle that’s why PQ and QR are hypotenuse for triangle PSQ and triangle QSR respectively. Always ignore negative values for a side of the triangle.