Question

In face centered cubic unit cell, edge length is:
a.) \[\dfrac{4}{\sqrt{3}}r\]
b.) \[\dfrac{4}{\sqrt{3}}r\]
c.) \[2r\]
d.) \[\dfrac{\sqrt{3}}{2}r\]

Answer 1

Hint: Question is talking about FCC from the solid state chapter, and here we have to find edge length in terms of radius of each atom for which we have to check the number of atoms on each edge or diagonal. And from a face centered cubic unit cell we can understand that it also has atoms on the face center.

Complete step by step solution:
Face-centered cubic lattice (fcc), like all lattices, has lattice points at the eight corners of the unit cell plus additional points at the centers of each face of the unit cell. The simplest crystal structures are those in which there is only a single atom at each lattice point.
 It has unit cell vectors a =b =c. The number of atoms in a unit cell is four (8×1/8 + 6×1/2 = 4). There are 26 metals that have the fcc lattice.
So, for finding edge length let’s assume length of edge is “a” and radius of atom is “r”.

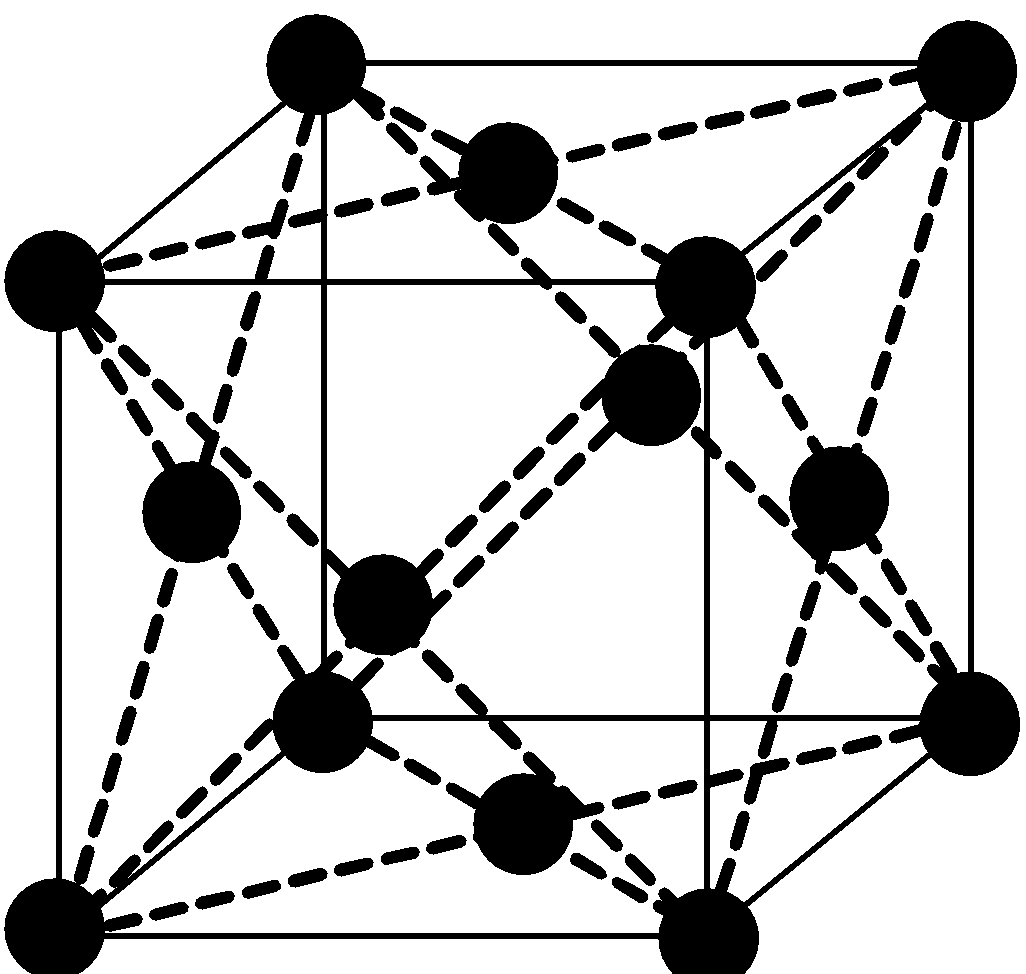
In FCC there is some gap between atoms which are on edge but there is no gap between the atoms on diagonal.
We will write the diagonal relation:
 \[\sqrt{3}\] x (edge of unit cell) = 4 x radius of atom
 \[\sqrt{3}\]a = 4 r
So, by rearranging:
‘a’ = \[\dfrac{4}{\sqrt{3}}\]r
Edge length of fcc unit cell = \[\dfrac{4}{\sqrt{3}}\]r

So, the correct answer is “Option A”.

Note: Here you should know that atoms on edge are not in contact with each other but atoms on diagonal are in touch with each other. In the fcc structures the spheres fill 74 % of the volume.