Question

In fcc structure, octahedral sites are present at:
A). Edge centres
B). Face centres
C). Body centers
D). Corners

Answer 1

Hint: The octahedral voids are located at the body centres and at the centres of the 12 edges of the cube. Number of octahedral voids per unit cell in a cubic close packing is 4.

Complete step-by-step answer:
-Let us consider the unit cell of cubic close packing lattice structure.

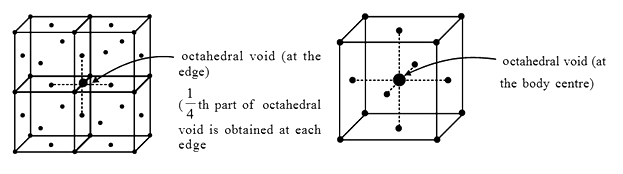
-The body centre of the cube is not occupied by any atom but its surrounded by six atoms at the face centres.
-If the atoms at the face centres are joined, a regular octahedron is generated.
-Thus, an octahedral void is located at the body center of the unit cell of ccp lattice.
-In addition to the octahedral void at the body centre there are 12 octahedral voids at the centres of the 12 edges of the cube.
-Each octahedral void on the edge centre is being shared by four unit cells.
-Thus, in cubic close packing the number of octahedral voids per unit cell can be calculated as under:
Number of octahedral voids per unit cell in a cubic close packing
= 1 (centre of the cubic) + 12 (at edge centres) x $1/4$
= 1 + 3 = 4
Clearly the answers are A and C.

Note: Do not confuse with the tetrahedral voids. There is one such void in the tetrahedron of ccp lattice. There are a total of eight tetrahedral voids in the unit cell of ccp structure. They are located on the body centres of the cube structure.