Question

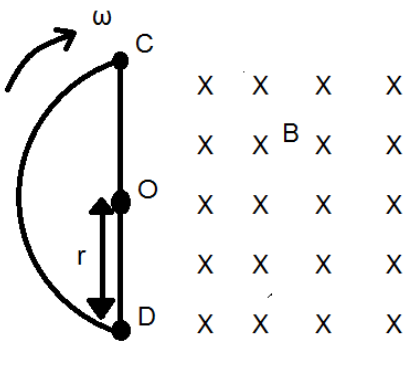
In fig, CODF is a semicircular loop of a conducting wire of resistance \[R\] and radius \[r\]. It is placed in a uniform magnetic field \[B\], which is directed into the page (perpendicular to the plane of the loop). The loop is rotated with a constant angular speed \[\omega \] about an axis passing through the centre \[O\] and perpendicular to the page. Then the induced current in the wire loop is:

A). 0
B). $\dfrac{B{{r}^{2}}\omega}{R}$
C). $\dfrac{B{{r}^{2}}\omega}{2R}$
D). $\dfrac{B{{r}^{2}}\pi \omega}{R}$

Answer 1

Hint: In order to solve this question, we are going to first find the change in the area for a small rotation of the wire through a small angle for a small time, after that the change in flux is calculated from dot product of area and magnetic field and thus, induced emf and current are found.
Formula used: The change in the flux of the magnetic field for a rotation though the area \[A\] and the magnetic field\[B\]is given by:
\[d\phi = B \cdot dA\]
Induced emf is given by
\[e = - \dfrac{{d\phi }}{{dt}}\]

Complete step-by-step solution:
Let us consider that the time taken for the wire to rotate through a small angle equal to\[d\theta \]is \[dt\]
Now, the change in the area for this much rotation is given by the formula
\[A = d\theta \left( {\dfrac{{\pi {r^2}}}{{2\pi }}} \right) = \dfrac{{d\theta }}{2}{r^2}\]
Now the change in the flux of the magnetic field for a rotation though the area\[A\]and the magnetic field\[B\]is given by:
\[d\phi = B \cdot dA\]
Putting the values in this equation, we get
\[d\phi = B \cdot dA = B\dfrac{{d\theta }}{2}{r^2}\]
Now the induced emf is the negative rate of change of the flux,
\[e = - \dfrac{{d\phi }}{{dt}}\]
Again putting the values in this equation,
\[e = - \dfrac{B}{2}\dfrac{{d\theta }}{{dt}}{r^2}\]
Now as we know that,
\[\dfrac{{d\theta }}{{dt}} = \omega \]
Hence by substituting the value of \[\dfrac{{d\theta }}{{dt}}\], we get
\[e = - \dfrac{B}{2}\omega {r^2}\]
Now we know that current induced in a conductor is given by the formula
\[i = - \dfrac{e}{R}\]
Thus, by substituting we get the induced current in the wire loop as
\[i = \dfrac{{B\omega {r^2}}}{{2R}}\]
Thus option (c) is correct.

Note: It is important to note that the current produced in a conductor due to change in magnetic flux through the region is called induced current. Magnetic flux is a product of magnetic field and area of Cross section. Like current produced in a generator is induced current. The change in the flux for the rotation is to be found carefully.