Question

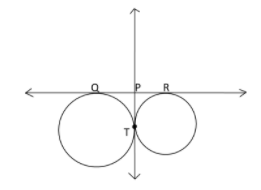
In figure, QR is a common tangent to the given circles, touching externally at the point T. The tangent at T meets QR at P. If $PT = 3.8cm$, then find the length of QR.

Answer 1

Hint: Observe the tangents drawn to both the circles. Use the theorem, the lengths of tangents drawn from an external point to a circle are equal. You will obtain $QR = 2PT$.

Complete step-by-step answer:

          

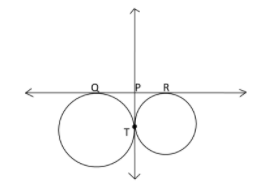
Two circles can be seen in the figure. For better understanding, lets name the bigger circle ${C_1}$and the smaller circle ${C_2}$.
We can see that tangents PQ and PT are drawn from an external point P to the circle ${C_1}$.
So,
$PQ = PT$ ---(1)
{Lengths of tangents drawn from an external point to a circle are equal.}
Similarly,
Tangents PR and PT are drawn to the circle ${C_2}$from an external point P;
Again using the same theorem,
$PR = PT$ ----(2)
QR can be written as
$QR = QP + PR$ ---(3)
Substituting the values of PQ and PR from equations (1) and (2) respectively, in equation (3),
We obtain,
$
  QR = PT + PT \\
  QR = 2PT \\
 $
Given that $PT = 3.8cm$
So,
$
  QR = 2 \times 3.8 \\
  QR = 7.6cm \\
 $

Note: It should be noted that in such type of questions, one must not confuse tangent and secant; a tangent to a circle is a straight line in the plane of circle, which touches the circle at only one point whereas secant to a circle intersects it at two distinct point. The theorems of tangent to a circle should not be applied on a secant as the results will be wrong.