Question

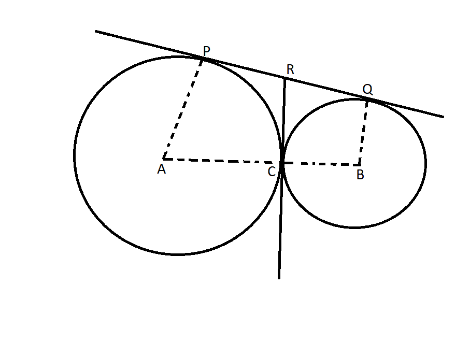
In figure, two circles touch each other at the point C. Prove that the common tangent to the circles at C, bisects the common tangent at P and Q.

Answer 1

Hint: From the figure, circles are touching each other from outside. We can prove the required statement using the concept of tangent and a point lies outside the circle.

Complete step-by-step answer:
Here we are given that two circles touch each other at point C
Since, we know that lengths of tangent drawn from an external point to a circle are equal.
So consider circle with centre A
According to external point theorem
RP=RC
Similarly consider circle with centre B
RQ=RC
$\therefore RP = RC$ and $RC = RQ$
$ \to RP = RQ$
Hence we can say that R is the mid-point of P and Q
Hence the common tangent to the circles at C, bisects the common tangent at P and Q.

Note: Circles can touch each other internally and externally but the concept of tangent has been used and tangent cannot pass through the inside circle. Definition of tangent is given as a straight line or plane that touches a curve or curved surface at a point, but if extended does not cross it at that point.