
In Fresnel’s bi-prism experiment, a mica sheet of refractive index
A).
B).
C).
D).
Answer
457.2k+ views
Hint: We know that introducing a mica sheet produces a path difference in the beam. In such a case, arrive at an expression for the path difference in terms of the material introduced and another expression for the same in terms of the geometric configuration of the beam in the experimental setup. Equate the two expressions and evaluate them to arrive at an expression for the wavelength of the light used, following which you can plug in the given values to arrive at the appropriate result.
Formula Used:
Fringe width:
Path difference:
Complete step-by-step solution:
We know that a Fresnel’s biprism is essentially an optical device that is used to observe interference of light and can be used to determine the wavelength of light incident on it. The biprism is made by joining the bases of two thin prisms together. When a monochromatic light source
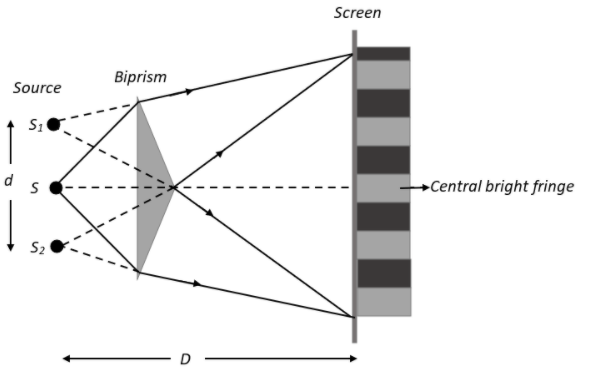
The fringes formed are of equal width, and the fringe width
We are given that a mica sheet of refractive index
But we know that if
Equating the above two expressions:
Multiplying and dividing the RHS of the above equation with
But we know that
Now, given that the central fringe gets shifted by 5 fringe widths, this means that the position of the beam also gets shifted through this width, i.e.,
Plugging this in to our previous equation we get:
Substituting the given values into the above equation, we can get the wavelength of the light used as:
Therefore, the correct choice is A.
Note: Let us understand the role of the biprism in the above experiment. The Fresnel biprism is used to essentially divide the wavefront of a monochromatic beam of light in such a way that it produces images that serve as two coherent virtual sources of the same light to consequently obtain a well resolved interference pattern. This is why experiments involving finding the wavelength of a source of light preferably involve Fresnel’s biprism instead of the Young's double slit apparatus. The biprism eliminates the difficulty associated with setting up the extended secondary slits to produce coherent beams of light. However, the biprism experiment is entirely based on the principles of Young’s experiment and follows calculations consistent with the latter.
Formula Used:
Fringe width:
Path difference:
Complete step-by-step solution:
We know that a Fresnel’s biprism is essentially an optical device that is used to observe interference of light and can be used to determine the wavelength of light incident on it. The biprism is made by joining the bases of two thin prisms together. When a monochromatic light source

The fringes formed are of equal width, and the fringe width
We are given that a mica sheet of refractive index
But we know that if
Equating the above two expressions:
Multiplying and dividing the RHS of the above equation with
But we know that
Now, given that the central fringe gets shifted by 5 fringe widths, this means that the position of the beam also gets shifted through this width, i.e.,
Plugging this in to our previous equation we get:
Substituting the given values into the above equation, we can get the wavelength of the light used as:
Therefore, the correct choice is A.
Note: Let us understand the role of the biprism in the above experiment. The Fresnel biprism is used to essentially divide the wavefront of a monochromatic beam of light in such a way that it produces images that serve as two coherent virtual sources of the same light to consequently obtain a well resolved interference pattern. This is why experiments involving finding the wavelength of a source of light preferably involve Fresnel’s biprism instead of the Young's double slit apparatus. The biprism eliminates the difficulty associated with setting up the extended secondary slits to produce coherent beams of light. However, the biprism experiment is entirely based on the principles of Young’s experiment and follows calculations consistent with the latter.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




