Question

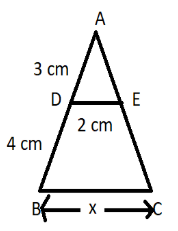
In given figure , if DE|| BC, then the value of x is equal to

(A). 3 cm
(B). 4 cm
(C). 7 cm
(D). 4.7 cm

Answer 1

Hint - To find x, prove triangle ADE is similar to ABC by using the information that DE || BC and then find out the value of x.

Complete step-by-step solution -
Given a triangle ABC, D and E are the points on sides AB and AC respectively. Also, DE || BC.
Now in triangles ADE and ABC-
$\angle D = \angle B$ (As DE || BC)
$\angle E = \angle C$ (As DE || BC)
$\therefore \vartriangle ADE \sim \vartriangle ABC$
So, we can write that-
$\dfrac{{AD}}{{AB}} = \dfrac{{DE}}{{BC}}$ { $\therefore \vartriangle ADE \sim \vartriangle ABC$ }
Now from figure, AD = 3 cm, DE = 2 cm and BD = 4 cm.
So, AB = AD + BD = 3 + 4 = 7 cm.
So, putting the value of AD, AB and DE we get-
$
  \dfrac{3}{7} = \dfrac{2}{x} \\
   \Rightarrow x = \dfrac{2}{3} \times 7 = \dfrac{{14}}{3} = 4.7 \\
 $
Hence, the value x is 4.7 cm.
Therefore, the correct option is D.

Note – Whenever such types of questions appear, always write down the things given in the question and then by using the properties of similar triangle and by using the condition that DE || BC, find the value of x.