Question

In Hertz experiment the ______________ of the electromagnetic waves is equal to the kinetic energy of the charges oscillating between two spheres.
A. Frequency
B. Energy
C. Wavelength
D. Velocity

Answer 1

Hint: Firstly, we could recall the experimental principle as well as the resultant observation. Doing so, you will understand that it is the oscillating electric charges that results in the production of the electromagnetic waves in the experiment. Thereby, you could find which quantity of EM wave is equivalent to the kinetic energy of the charges.

Complete answer:
In the question, we asked to find the property of electromagnetic waves that is equal to the kinetic energy of the charges oscillating between the two spheres in Hertz experiment.
In order to answer this let us first understand what Hertz experiment is. The experimental setup can be represented by the diagram below.

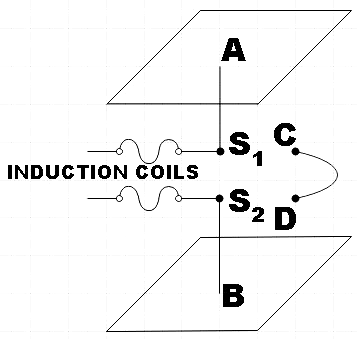
In the experimental setup we have two metallic plates of equal size held parallel to each other. They are further connected to two spheres ${{S}_{1}}$ and${{S}_{2}}$ by thick metallic rods. The spheres are charged to high value with the help of an induction coil. The resultant high potential difference across them ionizes the air in between them and thereby allowing a path for discharge of plates which further causes a spark.
So, oscillating electric fields are generated in between this gap which further generates oscillating magnetic fields. This is how Hertz experiment generates electromagnetic waves.
Also, the kinetic energy of the charges oscillating between the spheres is found to be equal to the energy of the electromagnetic waves in this experiment.

Hence, we found that option B is the correct answer.

Note:
This experiment proved that oscillating electric charges produce EM waves. Another observation was that the distance of oscillation is found to be very closely related to radiation wavelength. The resonance frequency of this experimental setup was found to be,
$\nu =\dfrac{1}{2\pi \sqrt{LC}}$