Question

In isosceles triangle \[\text{ABC}\], \[\text{AB} = \text{AC}\], a circle drawn taking
\[\text{AB}\] as a diameter meets the side \[\text{BC}\] at a point
\[D\]. if \[BD\ = 4\ cm\] . Let us find the value of \[\text{CD}\] ?

Answer 1

Hint: In this question, we need to find the value of \[\text{CD}\]. The triangle given in the question is an isosceles triangle. An isosceles triangle is nothing but a triangle whose length of any two sides is equal. First, we need to construct a triangle inscribed with the circle with centre \[O\] . If \[\text{BD}\] is \[4\ cm\] , we have the find \[\text{CD}\] . Also, we must know about the circle theorem . Circle theorem states that the angle inscribed on a semicircle is equal to \[90^{o}\] . Then from RHS congruence criteria on the triangles we can find the value of \[\text{CD}\].

Complete step by step solution:
Let us consider an isosceles triangle \[\text{ABC}\] whose sides \[\text{AB}\] and \[\text{AC}\] are of equal length that is \[\text{AB}=\text{AC}\]. Then let us make \[E\] in the middle of the side \[\text{AB}\]. Now, let us draw a circle with centre \[O\] and radius equal to the length of \[\text{AE}\]. Also, let us take the point at which the circle is cutting the line \[\text{BC}\], as \[D\] . Then we can draw a line \[\text{AD}\] on \[\text{BC}\] .

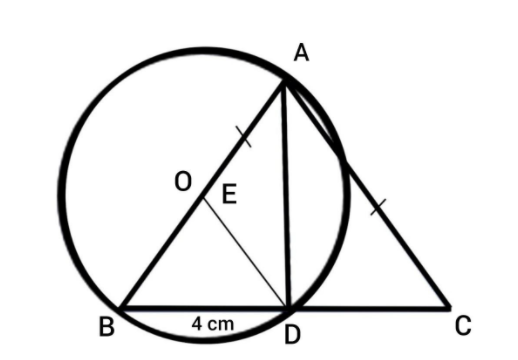
If \[\text{AB}\] is the diameter of the circle, then the radius of the circle is \[\dfrac{1}{2}{\text AB}\].
From the diagram, we can say that \[EB = ED = \dfrac{1}{2}\text{AB}\]
Then from the circle theorem, an angle inscribed on a semicircle is always equal to \[90^{o}\] . Therefore \[\angle \text{BDA} = 90^{o}\] . as \[\angle \text{BDA} = 90^{o}\], \[\angle \text{ADC} = 90^{o}\] .
Thus the triangle \[\text{EBD}\] is congruent to the triangle \[\text{ABC}\]
\[\Rightarrow \ \Delta EBD\ \cong \Delta ABC\]
Now on applying RHS congruence criteria on the triangles \[\text{EBD}\] and \[\text{ABC}\].
1. \[\text{AB} = \text{AC}\]
2. \[\text{AD}\] is common.
3. Both angles \[\angle \text{ADB}\ = \ \angle \text{ADC}\ = \ 90^{o}\]
Therefore,
\[\text{BD}\] is equal to \[\text{CD}\] (CPCT)
Since \[\text{BD}\] is equal to \[\text{CD}\]. Thus \[\text{CD}\] is \[4\ cm\].
Thus the value of \[\text{CD}\] is \[4\ cm\].
The value of \[\text{CD}\] is \[4\ cm\].

Note:
For solving this problem we need to know about the Congruence of the triangles . Two triangles are said to be congruent to each other if all three corresponding sides are equal and all the three corresponding angles are equal in measure. RHS stands for Right angle- Hypotenuse-Side .If the hypotenuse and a side of a right- angled triangle is equivalent to the hypotenuse and a side of the second right- angled triangle, then the two right triangles are said to be congruent by RHS rule. Here CPCT stands for Corresponding parts of Congruent triangles.