
In parallel combination of n cells, we obtain:
(A) More voltage
(B) More current
(C) Less voltage
(D) Less current
Answer
468.6k+ views
Hint: When n cells are connected in parallel combination, the internal resistance of n individual cells taken together is reduced as we know that when resistances are connected in parallel, the equivalent resistance decreases as a result current increases.
Complete step by step answer:
Let us consider n cells connected in parallel combination, to make the calculations simple let the voltage across their positive and negative terminals or emf (electromotive force) be equal,
And their internal resistance be,
The circuit below shows n cells connected in parallel across a resistance R, with current I flowing in the circuit.
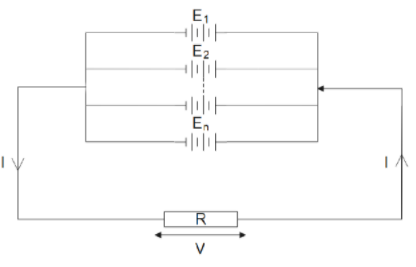
The emf of n cells connected in parallel will be equal to the emf of individual cell i.e. E.
Now, let us calculate the equivalent internal resistance of n cells, we get,
Thus, we see that the equivalent internal resistance of n cells is the internal resistance of an individual cell divided by n. The resistance in the equivalent circuit thus decreases and hence the current in the circuit increases.
Therefore, the correct answer is option (B).
Additional Information:
When n cells are connected in series combination, the equivalent emf is equal to the sum of individual emf,
And the equivalent internal resistance of n cells is,
Thus, we see in series combination the current in the circuit decreases as the equivalent internal resistance is n multiplied by resistance of an individual cell.
Note:
When the resistance to current flow in the circuit is increased the current in the circuit decreases and when the resistance to current flow in the circuit is decreased the current in the circuit increases, as according to Ohm’s law (
Complete step by step answer:
Let us consider n cells connected in parallel combination, to make the calculations simple let the voltage across their positive and negative terminals or emf (electromotive force) be equal,
And their internal resistance be,
The circuit below shows n cells connected in parallel across a resistance R, with current I flowing in the circuit.

The emf of n cells connected in parallel will be equal to the emf of individual cell i.e. E.
Now, let us calculate the equivalent internal resistance of n cells, we get,
Thus, we see that the equivalent internal resistance of n cells is the internal resistance of an individual cell divided by n. The resistance in the equivalent circuit thus decreases and hence the current in the circuit increases.
Therefore, the correct answer is option (B).
Additional Information:
When n cells are connected in series combination, the equivalent emf is equal to the sum of individual emf,
And the equivalent internal resistance of n cells is,
Thus, we see in series combination the current in the circuit decreases as the equivalent internal resistance is n multiplied by resistance of an individual cell.
Note:
When the resistance to current flow in the circuit is increased the current in the circuit decreases and when the resistance to current flow in the circuit is decreased the current in the circuit increases, as according to Ohm’s law (
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




