Question

In the below given problem, if 15.0 cm of water and spirit each are further poured into the respective arms of the tube, what is the difference in the levels of mercury in the two arms ? (Specific gravity of mercury = 13.6)
Problem: A U-tube contains water and methylated spirit separated by mercury. The mercury columns in the two arms are in level with 10.0 cm of water in one arm and 12.5 cm of spirit in the other .

Answer 1

Hint: We need to find the difference in height of mercury column when the height of the other two fluids is increased. First we will calculate the pressure of the mercury column when its height is changed and then find the difference in the pressure exerted by the water and spirit column. Then we will equate the pressure difference with the pressure difference of mercury and thus we will get the difference in height of the mercury column.

Formula used:
Pressure,
$P=h\rho g$

Complete answer:
In the question it is said that we have a U – shaped tube and one arm of the tube is filled with water and the other arm is filled with methylated spirit. The fluids are separated by mercury.
 

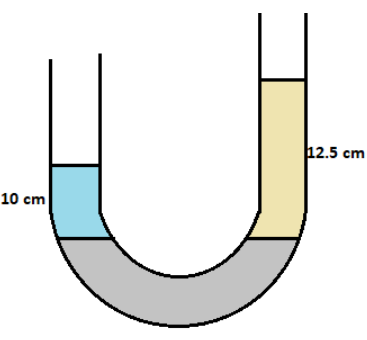
Let height of the water column be ‘${{h}_{w}}$’ and it is given as 10 cm
Let ‘${{h}_{s}}$’ be the height of the spirit column and it is given to be 12.5 cm.
In this case the height of the mercury column is said to be equal in both arms.
Now it is said that we add an extra amount of water and spirit to its respective columns, so that their height adds up by 15 cm.
Then the new height of water and spirit will become,
$\begin{align}
  & {{h}_{w}}=10+15=25cm \\
 & {{h}_{s}}=12.5+15=27.5cm \\
\end{align}$
Let us assume that ‘h’ is the difference in height caused in the mercury column.
We know pressure,
$P=h\rho g$, where ‘P’ is the pressure, ’h’ is the height, ‘$\rho $’ is density and ‘g’ is gravitational acceleration.
Then the pressure experienced by mercury can be given as,
${{P}_{m}}=h{{\rho }_{m}}g$ , here ‘${{P}_{m}}$’ is pressure difference of mercury and ‘${{\rho }_{m}}$’ is density of mercury.
We know density of mercury, ${{\rho }_{m}}=13.6g/c{{m}^{3}}$
Therefore pressure,
${{P}_{m}}=h\times 13.6\times g$
Similarly pressure of water column and spirit column can be written as,
$\begin{align}
  & {{P}_{w}}={{h}_{w}}{{\rho }_{w}}g \\
 & {{P}_{s}}={{h}_{s}}{{\rho }_{s}}g \\
\end{align}$
We know density of water, ${{\rho }_{w}}=1g/c{{m}^{3}}$ and density of methylated spirit, ${{\rho }_{s}}=0.8g/c{{m}^{3}}$
Now let us calculate the difference in pressure exerted by the water column and the spirit column.
$\begin{align}
  & {{P}_{w}}-{{P}_{s}}=\left( {{h}_{w}}{{\rho }_{w}}g-{{h}_{s}}{{\rho }_{s}}g \right) \\
 & {{P}_{w}}-{{P}_{s}}=g\left( {{h}_{w}}{{\rho }_{w}}-{{h}_{s}}{{\rho }_{s}} \right) \\
\end{align}$
By substituting the known values in the above equation, we get
$\begin{align}
  & {{P}_{w}}-{{P}_{s}}=g\left( 25\times 1-27.5\times 0.8 \right) \\
 & {{P}_{w}}-{{P}_{s}}=3g \\
\end{align}$
This is the pressure difference in the water and the spirit column..
We know that the difference in pressure by water and spirit is equal to the pressure difference of mercury.
Therefore by equating this we get,
$\begin{align}
  & {{P}_{m}}={{P}_{w}}-{{P}_{s}} \\
 & 13.6hg=3g \\
\end{align}$
$\begin{align}
  & h=\dfrac{3}{13.6} \\
 & h=0.22cm \\
\end{align}$
Therefore the difference in the level of mercury in the two arms is 0.22 cm.

Note:
We know that pressure is a scalar quantity defined as force applied per unit area and the force should be perpendicular to the area.
But fluid pressure is the measure of force per unit area of an object in a closed container or in a fluid.
According to Pascal’s law the pressure applied on a fluid will be transmitted throughout the fluid and to the walls of the container without any change in the magnitude of the pressure.