Question

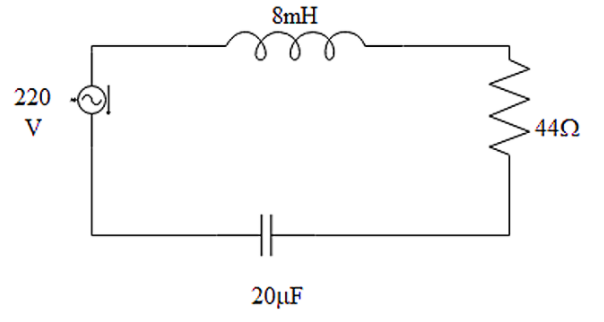
In the case of the series LCR circuit as represented in the diagram, what will be the resonance frequency and the amplitude of the current at the resonating frequency?

$\begin{align}
  & A.2500rad{{s}^{-1}}\text{ and }5\sqrt{2}A \\
 & B.2500rad{{s}^{-1}}\text{ and }5A \\
 & C.2500rad{{s}^{-1}}\text{ and }\dfrac{5}{\sqrt{2}}A \\
 & D.25rad{{s}^{-1}}\text{ and }5\sqrt{2}A \\
\end{align}$

Answer 1

Hint: The resonance frequency of the series LCR circuit can be found by taking the reciprocal of the square root of the value of inductance and the value of capacitance. Substitute the value in it and find the resonance frequency. Resonance current can be found by taking the ratio of the voltage and the value of resistance in the circuit. This can be helpful when answering the question.

Complete step by step solution:
As we all know, at the condition of resonance, the inductive reactance will be equivalent to the capacitive reactance.
${{X}_{L}}={{X}_{C}}$
Hence the total impedance of the resonance circuit can be found by the equation,
$Z=\sqrt{{{R}^{2}}+{{\left( {{X}_{L}}-{{X}_{C}} \right)}^{2}}}$
Substituting the relation between the capacitive and inductive reactance in this will give,
$Z=R$
The total impedance will be only resistance.
The resonance frequency of the series LCR circuit can be found by taking the reciprocal of the square root of the value of inductance and the value of capacitance.
This can be shown as an equation,
$\omega =\dfrac{1}{\sqrt{LC}}$
As the value of inductance connected in the circuit has been given as,
$L=8\times {{10}^{-3}}H$
And also the capacitance connected in the circuit can be shown as,
$C=20\times {{10}^{-6}}F$
Substituting these values in the equation can be written as,
\[\omega =\dfrac{1}{\sqrt{8\times {{10}^{-3}}\times 20\times {{10}^{-6}}}}=2500rad{{s}^{-1}}\]
Resonance current can be found by taking the ratio of the voltage and the value of resistance in the circuit. That is we can write that,
\[I=\dfrac{V}{R}\]
As the voltage of the circuit has been given as,
\[V=220V\]
And the resistance connected in the circuit has been mentioned as,
\[R=44\Omega \]
Therefore substituting these values in the equation will give the answer. That is,
\[I=\dfrac{220}{44}=5A\]
Therefore the resonance frequency and the resonance current have been calculated. The answer has been given as option B.
Therefore the resonance frequency and the resonance current have been calculated. The answer has been given as option B.

Note: An LCR circuit can be otherwise called a resonant circuit, RLC circuit, or a tuned circuit. This circuit can be defined as an electrical circuit, which includes an inductor, capacitor, and resistor which are connected in series or parallel. In this circuit, the resistance, current, and voltage phasors will be always in phase.