Question

In the circuit shown in figure, ammeter and voltmeter are ideal. If \[E = 4\;{\rm{V}}\], \[R = 9\;\Omega \]
 and \[r = 1\;\Omega \], then readings of ammeter and voltmeter are

A. \[{A_m} = 1\;{\rm{A}}\]
B. \[{A_m} = 2\;{\rm{A}}\]
C. \[{V_m} = 3\;{\rm{V}}\]
D. \[{V_m} = 4\;{\rm{V}}\]

Answer 1

Hint: The above problem can be resolved using the circuit analysis technique and the Kirchhoff’s Voltage rule. The significant calculations to the solution begin with finding the magnitude of the current through the ammeter. Then the current is used to determine the magnitude of voltage in the reading given by the voltmeter.

Complete step by step answer:
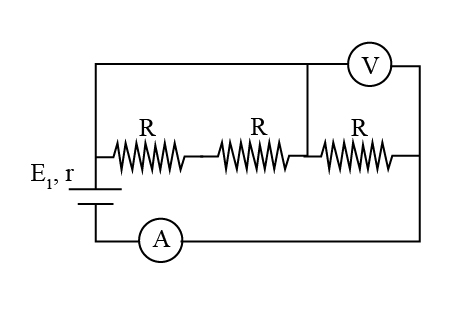
The magnitude of EMF is, \[E = 4\;{\rm{V}}\].
The internal resistance is, \[r = 1\;\Omega \].
The resistance is, \[R = 9\;\Omega \].
Considering the loop with the first two resistors, we can say that the current in two resistors will be equal and opposite to. Similarly, in the loop with the last two resistors, the current will be equal and opposite.
In the first resistor, the magnitude of current I flows from left to right.
In the second resistor, the magnitude of current I flows from right to left.
And, in the third resistor, the magnitude of current I flows from left to right.
Therefore, the current flow in the ammeter will be from right to left and the magnitude is
$I_1 = I+I+I$
$I_1 = 3I$
Then applying the KVL rule as,
\[\begin{array}{l}
E = {I_1} \times r + I \times R\\
4\;{\rm{V}} = 3I \times 1\;\Omega + I \times 9\;\Omega \\
I = \dfrac{1}{3}\;{\rm{A}}
\end{array}\]
The ammeter reading is, \[3I = 3 \times \dfrac{1}{3}\;{\rm{A}} = 1\;{\rm{A}}\].
And, the voltmeter reading is,
\[\begin{array}{l}
V = I \times R\\
V = \dfrac{1}{3}\;{\rm{A}} \times {\rm{9}}\;\Omega \\
V = 3\;{\rm{V}}
\end{array}\]
Therefore, the ammeter reading is 1 A and the voltmeter reading is 3 V

So, the correct answers are “Option A and C”.

Note:
To solve such a condition, one must be aware of the basic techniques to resolve the tricky circuit. The various methods like the Kirchhoff’s Current rule, and Kirchhoff’s Voltage rule need to be remembered significantly to resolve the complex circuits. The concepts and the applications for each of the methods need to be analysed firmly.