Question

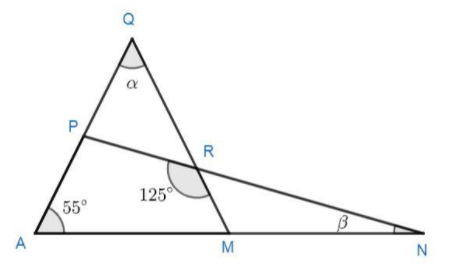
In the diagram AMN, QRM and PRN are all straight lines. The value of $\alpha + \beta $ is

Answer 1

Hint: Use the property of the triangle that the sum of the angles of the triangle is $180^\circ $in the triangle AQM, it gives:
\[\angle AQM{\text{ }} + \angle QAM + \angle AMQ{\text{ }} = {\text{ }}180^\circ \]
After that use the property of the sum of the linear pairs of angles, which says that if we have a pair of linear angles then their sum is$180^\circ $.

Complete step by step solution:
It is given in the problem that AMN, QRM, and PRN are all straight lines and we have to find the value of$\left( {\alpha + \beta } \right)$.
First, applying the angle sum property in triangle AQM,
We know that the sum of the angles in a triangle is always$180^\circ $. That is,
\[\angle AQM{\text{ }} + \angle QAM + \angle AMQ{\text{ }} = {\text{ }}180^\circ \]
Substitute the values of the given angles$\angle AQM = \alpha $and$\angle QAM = 55^\circ $into the equation.
\[\alpha {\text{ }} + 55^\circ + \angle AMQ{\text{ }} = {\text{ }}180^\circ \]
\[\angle AMQ{\text{ }} = {\text{ }}180^\circ {\text{ }}-{\text{ }}55^\circ {\text{ }} - {\text{ }}\alpha \]
On simplifying the above equation, we get
\[\angle AMQ = 125^\circ {\text{ }} - {\text{ }}\alpha \]
As we have given that AMN is a straight line, we know that the linear pair of angles have the sum$180^\circ $, then
$\angle $AMQ + $\angle $RMN = 180°
Now, substitute the values into the equation:
\[\;125^\circ {\text{ }}-{\text{ }}\alpha {\text{ }} + \angle RMN{\text{ }} = {\text{ }}180^\circ \]
\[\angle RMN{\text{ }} = {\text{ }}55^\circ {\text{ }} + {\text{ }}\alpha \]
It is also given to us in the problem that PRN is a straight line, so we know that the linear pair of angles have the sum $180^\circ $, then
\[\angle PRM{\text{ }} + \angle MRN{\text{ }} = {\text{ }}180^\circ \]
\[125^\circ {\text{ }} + \angle MRN{\text{ }} = {\text{ }}180^\circ \]
\[\angle MRN{\text{ }} = {\text{ }}55^\circ \]
We again use the property of the sum of the angles of the triangle MRN. Then we have,
\[\angle MRN{\text{ }} + \angle RMN + \angle RNM{\text{ }} = {\text{ }}180^\circ \]
Substitute the values into the equation:
\[55^\circ + 55^\circ + \alpha + \beta = 180^\circ \]
\[\alpha + \beta = 70^\circ \]

$\therefore$The required sum of angles have the value\[\alpha + \beta = 70^\circ \].

Note:
Try to find all the angles of the triangle RMN in terms of $\alpha $using the angle sum property and linear pair of angles property of the triangle.