Question

In the diagram shown, a light ray is incident on the lower medium boundary at an angle of ${45^0}$ with the normal. Which of the following statements is/are true?

This question has multiple correct options
$A.$ If $\dfrac{{{\mu _2}}}{{\sqrt 2 }}$, then angle of deviation is ${45^0}$
$B.$ If $\dfrac{{{\mu _2}}}{{\sqrt 2 }}$, then angle of deviation is ${90^0}$
$C.$ If $\dfrac{{{\mu _2}}}{{\sqrt 2 }}$, then angle of deviation is ${135^0}$
$D.$ If $\dfrac{{{\mu _2}}}{{\sqrt 2 }}$, then angle of deviation is ${0^0}$

Answer 1

HINT- In this question we will use the concept of total internal reflection. Total internal reflection (TIR) is the optical phenomenon in which the surface of the water in a fish tank (for example) when viewed from below the water level, reflects the underwater scene like a mirror, with no loss of brightness. In general, TIR occurs when waves in one medium reach the boundary with another medium at a sufficiently slanting angle, provided that the second medium is transparent to the waves and allows them to travel faster than in the first medium.

Step-By-Step answer:
Now coming back to question, Critical angle is given by:
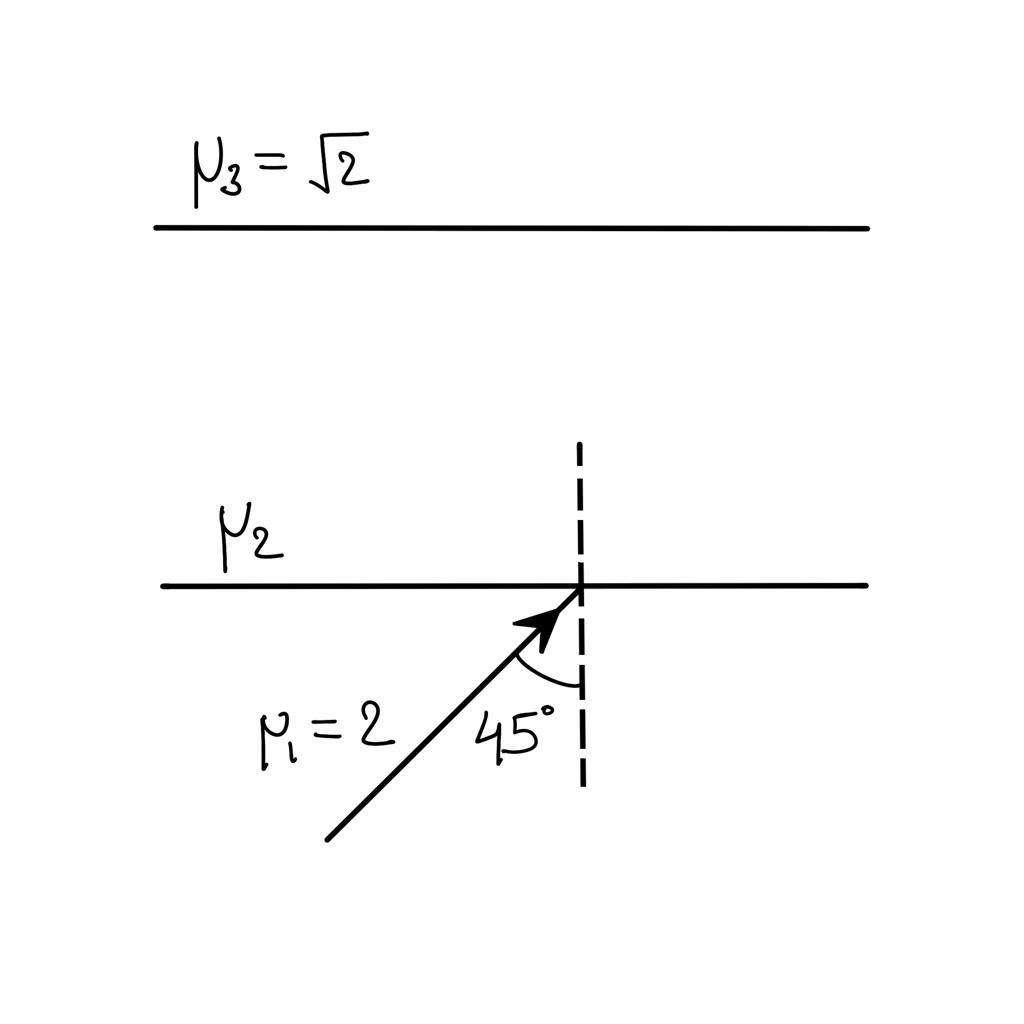
\[{\theta _c} = {\sin ^{ - 1}}(\dfrac{{{\mu _2}}}{{{\mu _1}}}) = {\sin ^{ - 1}}(\dfrac{{{\mu _2}}}{2})\]
If $\mu < \sqrt 2 $, then total internal reflection takes place and the ray reflects back, the angle of deviation is ${45^0} + {45^0} = {90^0}$
If $\mu = \sqrt 2 $, then the ray passes tangentially at the first medium. Then, the angle of deviation is ${45^0}$
If $\mu > \sqrt 2 $, then the ray enters the second medium and the angle of refraction at third interface is given by:
${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2} = {\mu _3}\sin {\theta _3}$
For 1st and 3rd medium,
$2\sin 45 = \sqrt 2 \sin {\theta _3}$
$\sin {\theta _3} = 1$
The angle of refraction is ${90^0}$
The deviation is $90 - 45 = {45^0}$
Therefore, option $A.$ and $B.$ are correct options for the above question.

NOTE- CRITICAL ANGLE
The angle of incidence beyond which rays of light passing through a denser medium to the surface of a less dense medium are no longer refracted but totally reflected.
So the critical angle is the angle of incidence that provides an angle of refraction of 90-degrees. For the crown glass-water boundary, the critical angle is 61.0 degrees. The actual value of the critical angle is dependent upon the combination of materials present on each side of the boundary.