
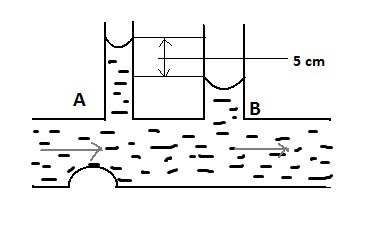
In the diagram shown below, the difference between the tubes of the manometer is 5 cm, the cross-sections at A and B are 6 sq mm and 10 sq mm respectively. The rate at which water flows through the tube is;($g = 10m{\operatorname{s} ^{ - 2}}$)
(A) 7.5 cc/sec
(B) 8.0 cc/sec.
(C) 10.0 cc/sec.
(D) 12.5 cc/sec.
Answer
233.1k+ views
Hint: This problem uses Bernoulli's theorem. Bernoulli's theorem is the pressure version of energy conservation. It is also similar to conservation of momentum.
Complete solution:
Bernoulli’s principle: In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different forms of Bernoulli's equation for different types of flow.
The simplest one being;
$P + \dfrac{1}{2}\rho {v^2} = C$.
Here, $P$ is the pressure at the surface of the liquid due to air, $\rho $ is the density of the fluid and v is the velocity of the fluid and C is constant.
Bernoulli's theorem also describes the relationship between a fluid's velocity and cross-sectional area. Mathematically it is written as ${A_1}{v_1} = {A_2}{v_2}$.
Now in this case, the difference between the tubes is given viz. 5cm= 0.05 meters.
So first we find the velocity relation in the two tubes.
Hence by applying Bernoulli’s theorem we get;
${A_1}{v_1} = {A_2}{v_2}$ here, ${A_1} = 6m{m^2}$ and ${A_2} = 10m{m^2}$ ;
Thus, $6{v_1} = 10{v_2}$
Thus ${v_1} = \dfrac{5}{3}{v_2}$ (equation:1)
Now apply Bernoulli’s theorem of conservation of pressure;
${P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2$
Solving the equation further we get;
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - {v_1}^2} \right)$
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - \dfrac{{25}}{9}{v_2}^2} \right)$ (from equation: 1)
Now we know that, ${P_2} - {P _1} = \rho g({h_2} - {h_1}) = 0.05\rho g$ (given)
$0.05\rho g = \dfrac{1}{2}\rho \left( {\dfrac{{16}}{9}{v_2}^2} \right)$
Solving the above equation we get,
${v_2} = 0.75m{s^{ - 2}}$
Therefore, rate of flow is mathematically Area X velocity;
Rate=${A_2}{v_2} = 75 \times {10^{ - 1}}c{m^3}{\sec ^{ - 1}}$
Hence option A is correct.
Note: (1) The units must be converted very carefully
(2) Av is the rate of flow of fluid so Bernoulli’s principle states that rate of flow is constant.
Complete solution:
Bernoulli’s principle: In fluid dynamics, Bernoulli's principle states that an increase in the speed of a fluid occurs simultaneously with a decrease in static pressure or a decrease in the fluid's potential energy. Bernoulli's principle can be applied to various types of fluid flow, resulting in various forms of Bernoulli's equation; there are different forms of Bernoulli's equation for different types of flow.
The simplest one being;
$P + \dfrac{1}{2}\rho {v^2} = C$.
Here, $P$ is the pressure at the surface of the liquid due to air, $\rho $ is the density of the fluid and v is the velocity of the fluid and C is constant.
Bernoulli's theorem also describes the relationship between a fluid's velocity and cross-sectional area. Mathematically it is written as ${A_1}{v_1} = {A_2}{v_2}$.
Now in this case, the difference between the tubes is given viz. 5cm= 0.05 meters.
So first we find the velocity relation in the two tubes.
Hence by applying Bernoulli’s theorem we get;
${A_1}{v_1} = {A_2}{v_2}$ here, ${A_1} = 6m{m^2}$ and ${A_2} = 10m{m^2}$ ;
Thus, $6{v_1} = 10{v_2}$
Thus ${v_1} = \dfrac{5}{3}{v_2}$ (equation:1)
Now apply Bernoulli’s theorem of conservation of pressure;
${P_1} + \dfrac{1}{2}\rho {v_1}^2 = {P_2} + \dfrac{1}{2}\rho {v_2}^2$
Solving the equation further we get;
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - {v_1}^2} \right)$
${P_1} - {P_2} = \dfrac{1}{2}\rho \left( {{v_2}^2 - \dfrac{{25}}{9}{v_2}^2} \right)$ (from equation: 1)
Now we know that, ${P_2} - {P _1} = \rho g({h_2} - {h_1}) = 0.05\rho g$ (given)
$0.05\rho g = \dfrac{1}{2}\rho \left( {\dfrac{{16}}{9}{v_2}^2} \right)$
Solving the above equation we get,
${v_2} = 0.75m{s^{ - 2}}$
Therefore, rate of flow is mathematically Area X velocity;
Rate=${A_2}{v_2} = 75 \times {10^{ - 1}}c{m^3}{\sec ^{ - 1}}$
Hence option A is correct.
Note: (1) The units must be converted very carefully
(2) Av is the rate of flow of fluid so Bernoulli’s principle states that rate of flow is constant.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




