Question

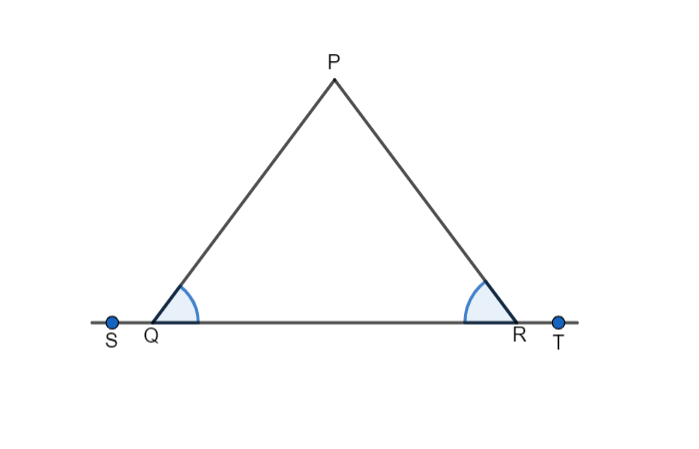
In the figure, \[\angle PQR = \angle PRQ\], then prove that \[\angle PQS = \angle PRT\].

Answer 1

Hint: Here, we will use the angle sum property of a triangle to find the measure of angle \[QPR\]. We will use the exterior angle property of a triangle to find the measure of angle \[PQS\] and angle \[PRT\]. We will compare their measures and prove that they are equal.

Complete step-by-step answer:

We know that in the triangle \[PQR\], \[\angle Q = \angle R\]. We will assume that measure of \[\angle Q = \angle R = x\].
We will apply the angle sum property of a triangle on triangle \[PQR\]. Therefore, we get
\[\begin{array}{l}\angle P + \angle Q + \angle R = 180^\circ \\ \Rightarrow x + \angle Q + x = 180^\circ \end{array}\]
We will solve the above equation and find the measure of angle \[Q\] in terms of \[x\].
Adding in the terms, we get
\[ \Rightarrow 2x + \angle Q = 180^\circ \]
Subtracting \[2x\] from both sides we get
\[\begin{array}{l} \Rightarrow 2x + \angle Q - 2x = 180^\circ - 2x\\ \Rightarrow \angle Q = 180^\circ - 2x{\rm{ }}\end{array}\]
As angle \[Q\] is equal to angle \[QPR\]. Therefore,
\[\angle Q = \angle QPR = 180^\circ - 2x\]……………………….\[\left( 1 \right)\]
We will apply the exterior angle property of a triangle on triangle \[PQR\] and find the measure of angle \[PQS\] in terms of \[x\].
\[\angle PQS = \angle QPR + \angle PQR\]
We will substitute the value of angle \[QPR\] from equation \[\left( 1 \right)\] in the above equation.
\[ \Rightarrow \angle PQS = 180^\circ - 2x + x\]
\[ \Rightarrow \angle PQS = 180^\circ - x\]…………………….\[\left( 2 \right)\]
We will apply the exterior angle property of a triangle on triangle \[PQR\] and find the measure of angle \[PRT\] in terms of \[x\].
Applying the exterior angle property, we get
\[\angle PQS = \angle QPR + \angle PRQ\]
We will substitute the value of angle \[QPR\] from equation \[\left( 1 \right)\] in the above equation:
\[ \Rightarrow \angle PRT = 180^\circ - 2x + x\]
Subtracting the like terms, we get
\[ \Rightarrow \angle PRT = 180^\circ - x\]………………………..\[\left( 3 \right)\]
We can see from equation \[\left( 2 \right)\] and equation \[\left( 3 \right)\] that:
\[ \Rightarrow \angle PQS = \angle PRT\]
$\therefore $ We have proved the required result.

Note: We know that sides opposite to equal angles are equal in length. So, we can say that the triangle given in the question has 2 equal sides and thus, is an isosceles triangle. We can conclude from this question that in an isosceles angle 2 exterior angles are equal.
In order to solve this question, we need to keep in mind following properties:
Angle Sum Property of a triangle: Sum of all angles of a triangle is \[{180^ \circ }\].
Exterior Angle Property of a triangle: The measure of any exterior angle of a triangle is the sum of its interior opposite angles.