Question

In the figure, CD is a diameter of the circle with centre O. Diameter CD is perpendicular to chord AB at point E. Show that $\Delta ABC$ is an isosceles triangle.

Answer 1

Hint: To do this question, we will first consider the two triangles formed in the triangle $\Delta ABC$, $\Delta ACE$ and $\Delta BCE$. Then we will try to prove these two triangles as congruent triangles. Then, as both these triangles will be congruent, we can say that the sides AC and BC are equal by the rule of CPCT. Thus, as two sides of a triangle will be equal, the triangle $\Delta ABC$ will be an isosceles triangle.

Complete step by step answer:
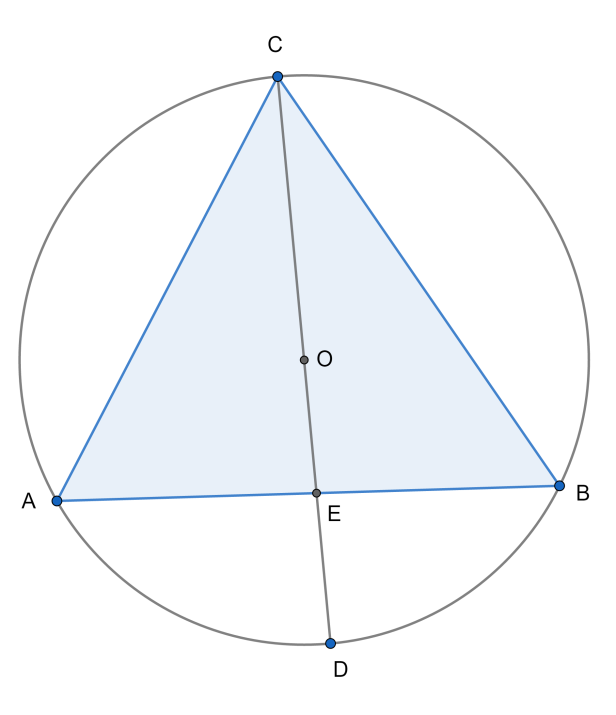
Here, we have been given the following figure:

In this figure, we have to prove that $\Delta ABC$ is an isosceles triangle.
For that, let us consider $\Delta ACE$ and $\Delta BCE$.
We can see in these two triangles that:
CE = CE (as CE is a common side to both the triangles)
$\angle AEC=\angle BEC={{90}^{\circ }}$ (as it has been given to us that the diameter CD is perpendicular to the chord AB at E)
AE = EB (we know that perpendicular from the centre to any chord of a triangle bisects the chord)
Thus, we can say that $\Delta ACE\cong \Delta BCE$ by the SAS (side angle side) criteria.
Hence, by applying CPCT (corresponding parts of congruent triangles) in these triangles, we can say that:
AC = BC
Thus, since two sides of the triangle $\Delta ABC$ are equal (AC and BC), we can say that the triangle $\Delta ABC$ is an isosceles triangle.
Hence, proved.
Note:
There are certain properties of a circle that might come in handy. They are given as follows:
1. Perpendicular on a chord from the circle always bisects the chord.
2. The line from the centre bisecting the chord is perpendicular to the chord.
3. Angle in a semicircle is ${{90}^{\circ }}$.
4. Angle subtended by any chord at the centre is double the angle subtended by that chord at any other point of the circle.
5. Angles subtended by the same chord at different points of the circles are equal.