Question

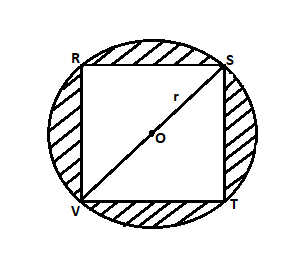
In the figure given below, $RSTV$ is a square inscribed in a circle $O$ and radius $r$. What is the area of the shaded region?

A.${r^2}\left( {\pi - 2} \right)$
B.$2r\left( {2 - \pi } \right)$
C.$\pi \left( {{r^2} - 2} \right)$
D.$\pi {r^2} - 8r$

Answer 1

Hint: Sides $RS$ and $RV$ or sides$ST$and $TV$ constructs a Right angled triangle with the help of the diagonal$SV$.

Complete step-by-step solution:
First of all in these types of questions, we will start the question by listing the given quantities in the question.
So, here in this question it is given that
A circle with center $O$ is drawn having a radius $r$,
Secondly, a square $RSTV$ is inscribed in that circle.
So, now we just have to find the area of the shaded region, which is nothing but the subtraction of the area of the square from the area of the circle.
That is, Area of the shaded region $ = $ Area of the circle$O$ $ - $ Area of the square $RSTV$ ……(i)
So, for solving this we need to know the area of the circle and the area of the square $RSTV$
And we know that the Area of the circle having radius $r$, would be $\pi {r^2}$.
So, now we just have to find the area of the square and then just by putting the values in the
equation (i), we will get our answer.
So, for finding the area of the square we just know that the diagonal of the square would be equal to $2r$ which can be seen in the diagram.
So, as we know that Sides $RS$ and $RV$ or sides$ST$and $TV$ constructs a Right angled triangle with the help of the diagonal$SV$.
So, $\vartriangle RST$and $\vartriangle STV$ are right angled triangles.
So, here we are just considering $\vartriangle STV$to find the side of the square $RSTV$
So, in $\vartriangle STV$
We know that side $SV = 2r$ ……{As proved above}
And sides $ST = TV$ …….{As they both sides of the square $RSTV$}
Now, let us assume that side $ST = TV = x$
$ \Rightarrow $By applying Pythagoras theorem on the right angled triangle, $\vartriangle STV$
We get, $S{T^2} + T{V^2} = S{V^2}$
$ \Rightarrow $By putting corresponding values we get
$\begin{gathered}
  {x^2} + {x^2} = {\left( {2r} \right)^2} \\
   \Rightarrow 2{x^2} = 4{r^2} \\
   \Rightarrow {x^2} = 2{r^2} \\
   \Rightarrow x = \sqrt {2{r^2}} \\
   \Rightarrow x = \sqrt 2 r \\
\end{gathered} $
$ \Rightarrow $Side of square $RSTV = \sqrt 2 r$
$ \Rightarrow $Area of square $RSTV = {\left( {side} \right)^2} = {\left( {\sqrt 2 r} \right)^2}$
$ \Rightarrow $Area of square $RSTV = 2{r^2}$
Now, by putting the values of area of square and area of circle in the equation (i)
We get
Area of the shaded region $ = $ Area of the circle$O$ $ - $ Area of the square $RSTV$
$ \Rightarrow $Area of the shaded region $ = \pi {r^2} - 2{r^2}$
$ \Rightarrow $Area of the shaded region $ = {r^2}\left( {\pi - 2} \right)$
$\therefore $Option A is the answer.

Note: In these type of questions of shaded region we can understand the geometry as if we are removing one area from another likewise in this question we can consider the circle and the square as two different diagrams and after finding their areas individually, we just have to remove the area of the square from the area of the circle.