
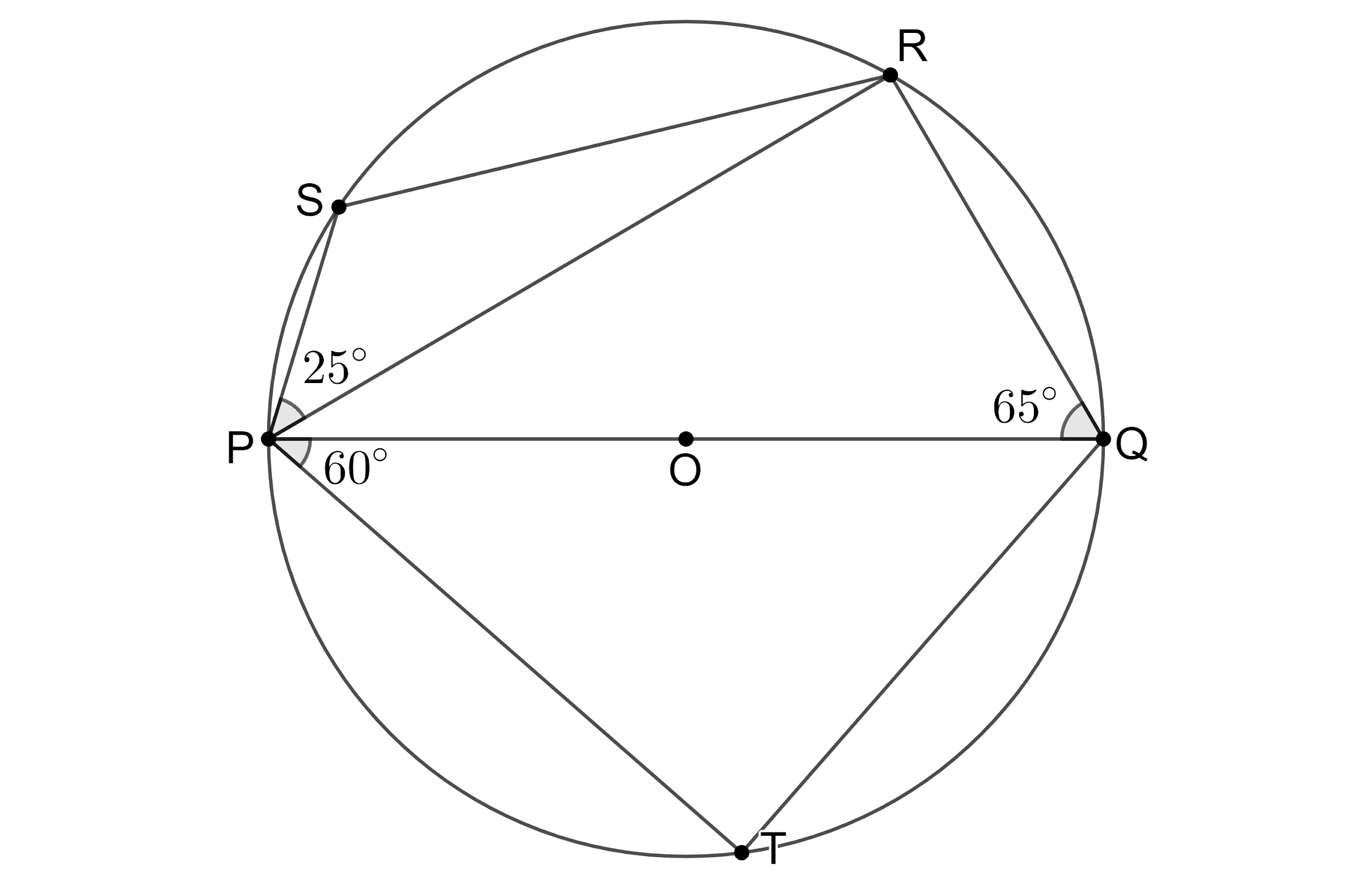
In the figure, PQ is the diameter of the circle. If $ \angle PQR={{65}^{\circ }} $ , $ \angle RPS={{25}^{\circ }} $ and $ \angle QPT={{60}^{\circ }} $ , then find the measure of (i) $ \angle QPR $ , (ii) $ \angle PRS $ , (iii) $ \angle PSR $ and (iv) $ \angle PQT $ ?

Answer
563.4k+ views
Hint: We start solving the problem by making use of the fact that angle in a semicircle is $ {{90}^{\circ }} $ to find the value of angle $ \angle QTP $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PQT to find the angle $ \angle PQT $ . We then make use of the fact that angle in a semicircle is $ {{90}^{\circ }} $ to find the value of angle $ \angle QRP $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PQR to find the angle $ \angle QPR $ . We then make use of the fact that the sum of opposite angles in a concyclic polynomial is $ {{180}^{\circ }} $ to find the angle $ \angle PSR $ . We then make use of the fact that the sum of the angles in a triangle is \[{{180}^{\circ }}\] for triangle PRS to find the angle \[\angle PRS\].
Complete step by step answer:
According to the problem, we are given that PQ is the diameter of the circle. If $ \angle PQR={{65}^{\circ }} $ , $ \angle RPS={{25}^{\circ }} $ and $ \angle QPT={{60}^{\circ }} $ . We need to find the values of the angles (i) $ \angle QPR $ , (ii) $ \angle PRS $ , (iii) $ \angle PSR $ and (iv) $ \angle PQT $ .
Let us redraw the given figure,
From the figure, we can see that $ \angle QTP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QTP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ so, we get $ \angle QTP={{90}^{\circ }} $ ---(1).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQT $ , we have $ \angle QTP+\angle TPQ+\angle PQT={{180}^{\circ }} $ .
From equation (1), we get
$ \Rightarrow {{60}^{\circ }}+{{90}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
$ \Rightarrow {{150}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
$ \Rightarrow \angle PQT={{30}^{\circ }} $ .
From the figure, we can see that $ \angle QRP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QRP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ , so we get $ \angle QRP={{90}^{\circ }} $ ---(2).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQR $ , we have $ \angle PQR+\angle QRP+\angle QPR={{180}^{\circ }} $ .
From equation (2), we get
$ \Rightarrow {{65}^{\circ }}+{{90}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
$ \Rightarrow {{155}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
$ \Rightarrow \angle QPR={{25}^{\circ }} $ .
We can see that the points P, Q, R, S form a concyclic quadrilateral. We know that the sum of opposite angles in a concyclic polynomial is $ {{180}^{\circ }} $.
So, we have $ \angle PQR+\angle PSR={{180}^{\circ }} $ .
$ \Rightarrow {{65}^{\circ }}+\angle PSR={{180}^{\circ }} $ .
$ \Rightarrow \angle PSR={{115}^{\circ }} $ ---(3).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From triangle $ PSR $ , we have $ \angle PSR+\angle PRS+\angle RPS={{180}^{\circ }} $ .
From equation (3), we get
$ \Rightarrow {{25}^{\circ }}+{{115}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
$ \Rightarrow {{140}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
$ \Rightarrow \angle PRS={{40}^{\circ }} $ .
$ \therefore $ We have found the values of angles $ \angle QPR $ , $ \angle PRS $ , $ \angle PSR $ and $ \angle PQT $ as $ {{25}^{\circ }} $ , $ {{40}^{\circ }} $ , $ {{115}^{\circ }} $ and $ {{30}^{\circ }} $ .
Note:
We can see that the given problem contains a huge amount of calculations, so we need to perform each step carefully to avoid confusion. We should not confuse angles while using the property of angle in a semi-circle. We should not make calculation mistakes while solving this problem. Whenever we get this type of problem, we should make use of properties of concyclic polygons and angle in a semi-circle to get the required answer.
Complete step by step answer:
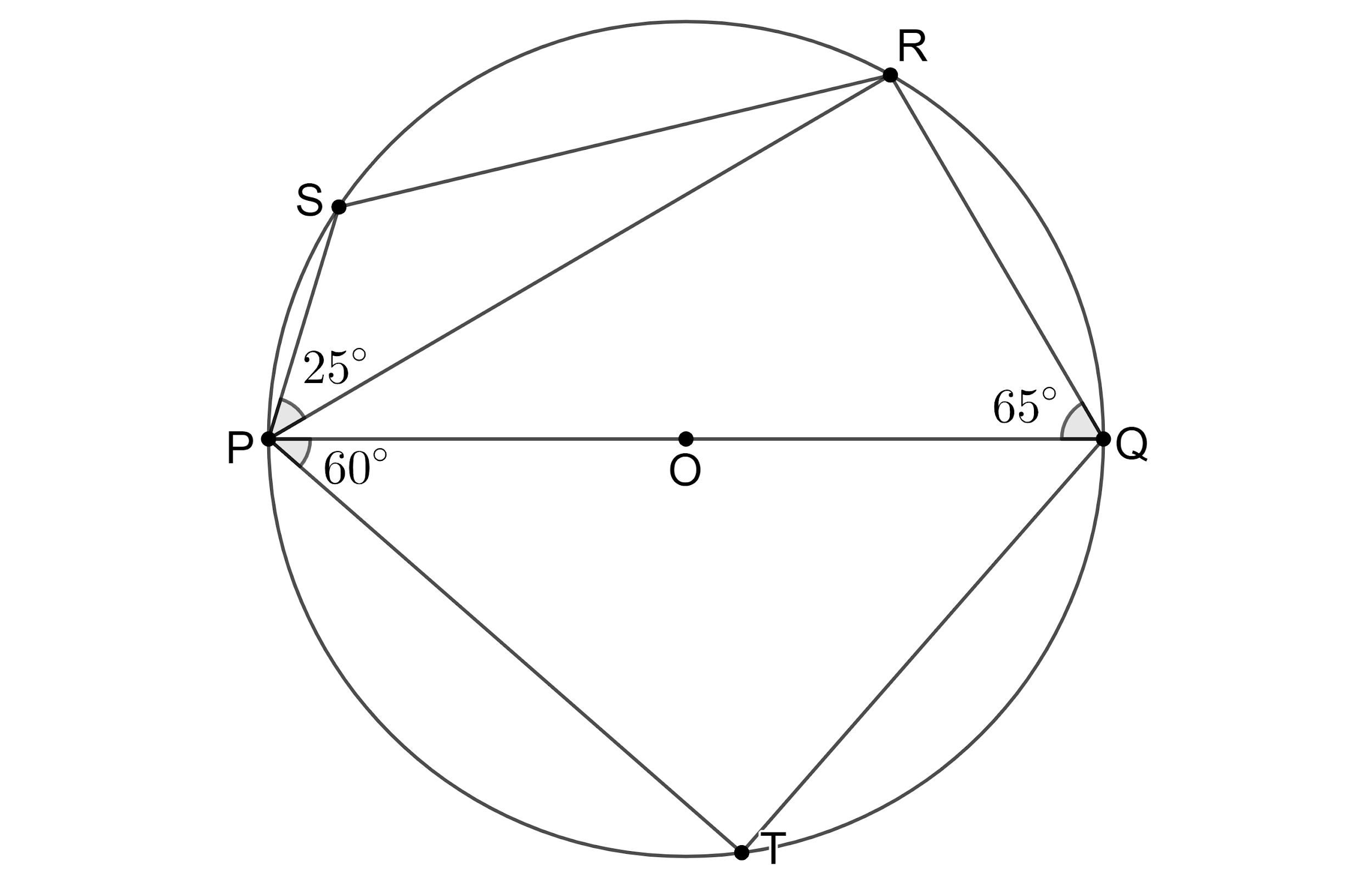
According to the problem, we are given that PQ is the diameter of the circle. If $ \angle PQR={{65}^{\circ }} $ , $ \angle RPS={{25}^{\circ }} $ and $ \angle QPT={{60}^{\circ }} $ . We need to find the values of the angles (i) $ \angle QPR $ , (ii) $ \angle PRS $ , (iii) $ \angle PSR $ and (iv) $ \angle PQT $ .
Let us redraw the given figure,

From the figure, we can see that $ \angle QTP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QTP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ so, we get $ \angle QTP={{90}^{\circ }} $ ---(1).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQT $ , we have $ \angle QTP+\angle TPQ+\angle PQT={{180}^{\circ }} $ .
From equation (1), we get
$ \Rightarrow {{60}^{\circ }}+{{90}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
$ \Rightarrow {{150}^{\circ }}+\angle PQT={{180}^{\circ }} $ .
$ \Rightarrow \angle PQT={{30}^{\circ }} $ .
From the figure, we can see that $ \angle QRP $ is the angle formed by connecting the ends of the diameter of the circle, which means that the angle $ \angle QRP $ is the angle in a semicircle. We know that angle in a semicircle is $ {{90}^{\circ }} $ , so we get $ \angle QRP={{90}^{\circ }} $ ---(2).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From the triangle $ PQR $ , we have $ \angle PQR+\angle QRP+\angle QPR={{180}^{\circ }} $ .
From equation (2), we get
$ \Rightarrow {{65}^{\circ }}+{{90}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
$ \Rightarrow {{155}^{\circ }}+\angle QPR={{180}^{\circ }} $ .
$ \Rightarrow \angle QPR={{25}^{\circ }} $ .
We can see that the points P, Q, R, S form a concyclic quadrilateral. We know that the sum of opposite angles in a concyclic polynomial is $ {{180}^{\circ }} $.
So, we have $ \angle PQR+\angle PSR={{180}^{\circ }} $ .
$ \Rightarrow {{65}^{\circ }}+\angle PSR={{180}^{\circ }} $ .
$ \Rightarrow \angle PSR={{115}^{\circ }} $ ---(3).
We know that the sum of the angles in a triangle is \[{{180}^{\circ }}\].
From triangle $ PSR $ , we have $ \angle PSR+\angle PRS+\angle RPS={{180}^{\circ }} $ .
From equation (3), we get
$ \Rightarrow {{25}^{\circ }}+{{115}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
$ \Rightarrow {{140}^{\circ }}+\angle PRS={{180}^{\circ }} $ .
$ \Rightarrow \angle PRS={{40}^{\circ }} $ .
$ \therefore $ We have found the values of angles $ \angle QPR $ , $ \angle PRS $ , $ \angle PSR $ and $ \angle PQT $ as $ {{25}^{\circ }} $ , $ {{40}^{\circ }} $ , $ {{115}^{\circ }} $ and $ {{30}^{\circ }} $ .
Note:
We can see that the given problem contains a huge amount of calculations, so we need to perform each step carefully to avoid confusion. We should not confuse angles while using the property of angle in a semi-circle. We should not make calculation mistakes while solving this problem. Whenever we get this type of problem, we should make use of properties of concyclic polygons and angle in a semi-circle to get the required answer.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Which are the Top 10 Largest Countries of the World?

What are the major means of transport Explain each class 12 social science CBSE

Draw a labelled sketch of the human eye class 12 physics CBSE

Why cannot DNA pass through cell membranes class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

Draw a neat and well labeled diagram of TS of ovary class 12 biology CBSE




