Question

In the figure, the potentiometer wire AB of length L and resistance 9r is joined to the cell D of e.m.f and internal resistance r. The cell C's e.m.f is $\dfrac{e}{2}$  and its internal resistance is 2r. The galvanometer G will show no deflection when the length AJ is

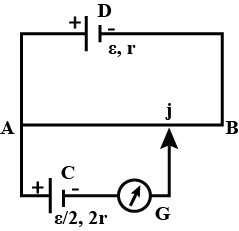
A) $\dfrac{{4L}}{9}$
B) $\dfrac{{5L}}{9}$
C) $\dfrac{{7L}}{{18}}$
D) $\dfrac{{11L}}{{18}}$

Answer 1

Hint: In the figure the potentiometer has no current flowing in between C and galvanometer then only there is no deflection. We have to calculate the length of AJ which is the difference of potential across A and J and then equating them with the potential gradient K by supposing the length of AJ be p. Then we will get our length of no deflection (p) cm or m.

Step by step solution:
Step 1:
A galvanometer works as an actuator, by producing a rotary deflection (of a "pointer"), in response to electric current flowing through a coil in a constant magnetic field. They were the first instruments used to detect and measure small amounts of electric currents.
Potential Gradient is the decrease in potential length per unit length. It is calculated as $\dfrac{V}{L}$ , where V is the potential difference between two points and L is the distance between two points. The longer the wire will make the lesser the potential gradient and the greater the sensitivity of the potentiometer.
Step 2:
Now coming to the question:
The galvanometer is showing no deflection. Let consider a point D between the galvanometer and C. Let the distance of A and J be p.
This implies the potential difference across D and J will be zero=${V_D}$ −${V_J}$ =0
We are given in question: The cell C's e.m.f is $\dfrac{e}{2}$  and its internal resistance is \[2\]r.
And also the potentiometer wire AB of length L and resistance \[9\]r 
Then total resistance will be \[10\]r.
Calculating the I(current) is $\dfrac{E}{r}$ =$\dfrac{E}{{10r}}$
Potential across AJ will be the sum of difference of potential difference between A and D, and D and J
This implies ${V_{AJ}}$ =$\left( {{V_A} - {V_D}} \right) + \left( {{V_D} - {V_J}} \right)$ and potential difference across D and J is zero.
So, ${V_A}$−${V_J}$ =$\dfrac{E}{2} + 0$ (we are given cell C's e.m.f is $\dfrac{e}{2}$  )
Now, potential gradient (K) is equal to $\dfrac{{I \times 9r}}{L}$
Putting the value of I we will get K=$\dfrac{9}{{10}}\dfrac{E}{L}\dfrac{{volt}}{{meter}}$
We have assumed the distance of A and J is p then K multiplied by p equals to $\dfrac{E}{2}$
Then p(length)= $\dfrac{{9E}}{{10L}} \times \dfrac{2}{E}$ which on solving give length equal to $\dfrac{{5L}}{9}$

Hence option B is correct.

Note:These are formula based questions. One needs to have a knowledge of potentiometer, galvanometer, the flowing of a current, and most important the potential gradient. The characteristics of a potentiometer are important and without that it is hard to solve such a question. Therefore it is advised to learn the definition and working then only the diagram will reveal the solution automatically.