Question

In the figure $\theta = {\tan ^{ - 1}}\sqrt 2 $, then the correct direction of the magnetic field at p can be shown by the arrow

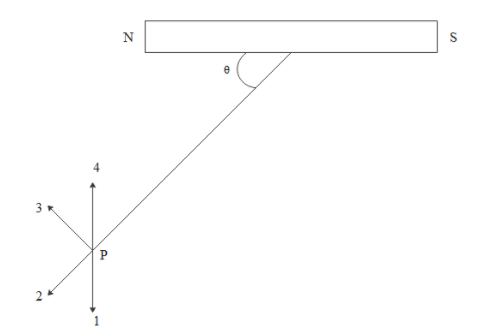
A. 2
B. 4
C. 1
D. 3

Answer 1

Hint: Magnets will be having two poles definitely. Unipolar magnets don't exist. Just like electric dipoles we can consider magnetic dipoles. In a magnetic dipole, the magnetic moment vector goes from south pole to north pole inside the magnet. We resolve that along axial and equatorial to get the magnetic fields.
Formula used-
$\eqalign{
  & {B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{r^3}}} \cr
  & {B_{equitorial}} = - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{r^3}}} \cr} $

Complete answer:
When charge is at rest it produces only electric fields but when charge is under motion it produces both electric and magnetic fields. So a current carrying produces a magnetic field. Due to this magnetic field magnetic moment also produced.
Similarly magnetism can be produced by magnets themselves and due to the magnets, magnetic fields are produced.
The position of the point determines the direction of the magnetic field.
If the point is located on the axis then we have one formula to calculate the magnetic field over there and if the point is located on the equatorial point then we have another formula for magnetic field.
For axial point the magnetic field will be
${B_{axial}} = \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{{2M}}{{{r^3}}}$
‘r’ is the distance between the center of magnet and the point P.
So the magnetic field will be along the direction of magnetic moment vector(M)
For equatorial point the magnetic field will be
${B_{equitorial}} = - \dfrac{{{\mu _0}}}{{4\pi }}\dfrac{M}{{{r^3}}}$
So the equatorial magnetic field will be anti parallel to the direction of magnetic moment vector(M)
If we refer below diagram

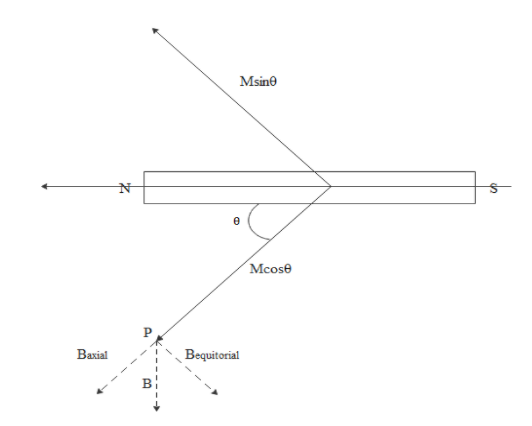
$M\cos \theta $ will be the axial magnetic moment vector and axial magnetic field will be along $M\cos \theta $ at P.
$M\sin \theta $ will be equatorial magnetic moment vector and equatorial magnetic field will be anti parallel to $M\sin \theta $ at P.
So the resultant magnetic field will be vertically downward.
That is along the vector 1 from the below diagram.

Hence option C is correct.

Note:
The point which they had given is not a perfect axial point nor a perfect equatorial point. It is an oblique point. So we will resolve the magnetic moment vector into axial direction and along the equatorial direction. After resolving we had found out the direction of magnetic field components at that point and found the resultant.