Question

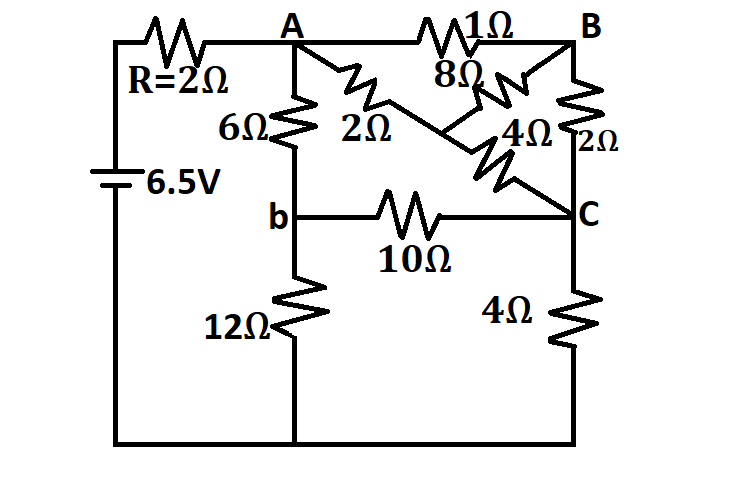
In the following circuit, the current through the resistor R (=2$\Omega $) is I amperes. The value of I is:

Answer 1

Hint: It is advisable to solve the question by taking one part of the circuit at a time. By doing so we can simplify this complex circuit. It is also observable that the circuit can be simplified into the balanced Wheatstone bridge. The Wheatstone bridge can be analysed clearly as two series of strings in parallel when balanced. In our Resistors in Series tutorial, we saw that as a result of the current flowing through it as described by Ohms Law, each resistor inside the series chain causes an IR drop, or voltage drop through itself. We can solve a balanced Wheatstone bridge easily as the resistance at the junction can be neglected in this case.

Complete answer:
Let us solve the question part by part.
If we observe the network, we can see that it is a case of a balanced Wheatstone bridge. (Refer to the diagram to find the balanced Wheatstone bridge)

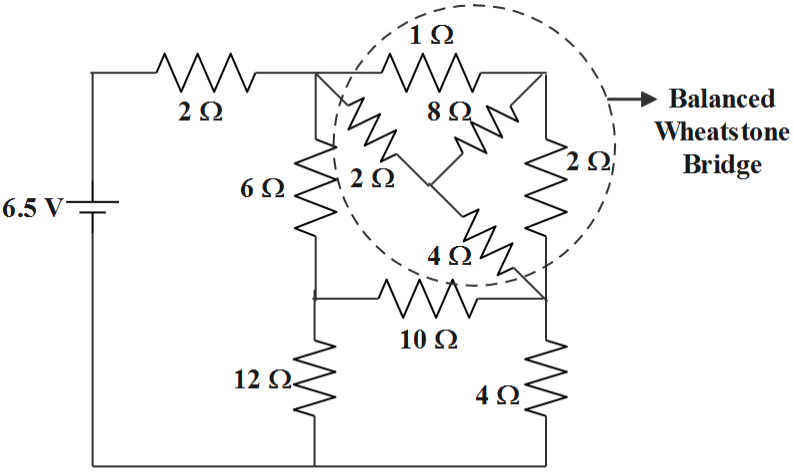
So, now
The equivalent resistance of balanced Wheatstone bridge is
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{2+1}+\dfrac{1}{2+4}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{3}+\dfrac{1}{6}$
\[\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{2+1}{6}\]
\[\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{2}\]
\[\Rightarrow {{R}_{eq}}=2\Omega \]
Now,
The new circuit will look like

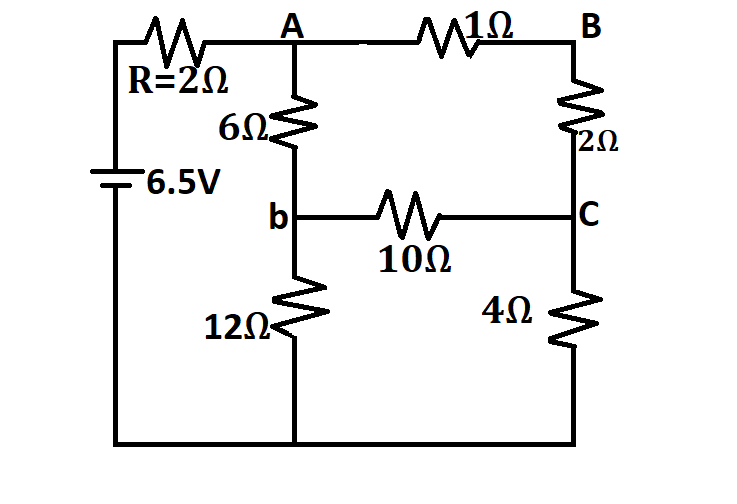
Now, In this new circuit we can see a new balanced Wheatstone Bridge again

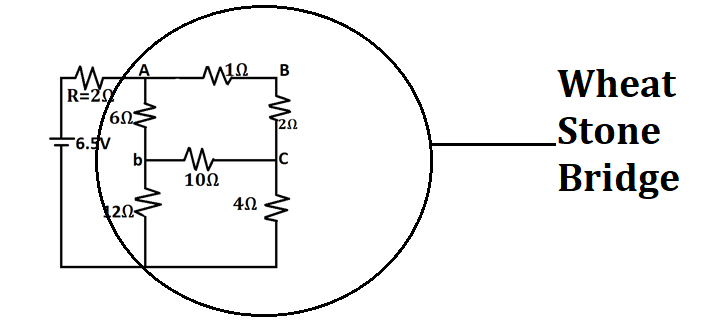
Again, The equivalent resistance of balanced Wheatstone bridge is
$\dfrac{1}{{{R}_{eq}}}=\dfrac{1}{12+6}+\dfrac{1}{2+4}$
$\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1}{18}+\dfrac{1}{6}$
\[\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{1+3}{18}\]
\[\Rightarrow \dfrac{1}{{{R}_{eq}}}=\dfrac{2}{9}\]
\[\Rightarrow {{R}_{eq}}=\dfrac{9}{2}\Omega \]
Now, the total resistance of the circuit will be
\[\Rightarrow {{R}_{eq}}=(2+4.5)\Omega \]
\[\Rightarrow {{R}_{eq}}=6.5\Omega \]
Therefore,
By ohm’s law
We have,
V = IR
So,
$I=\dfrac{V}{R}$
Here,
V = 6.5 V
And R = \[6.5\Omega \]
So, using the values we have
$\Rightarrow I=\dfrac{6.5}{6.5}$
$\Rightarrow I=1A$
So, the value of I in the given circuit will be 1A

Note:
While solving such a question, remember that it is easier to simplify the circuit first. Try taking out the resistances which are useless such as in this case the ones that were rejected due to the balancing of the Wheatstone bridge. Sometimes, the fuses in the circuit are fuse ones which can also be neglected.