
In the given circuit, the AC source has
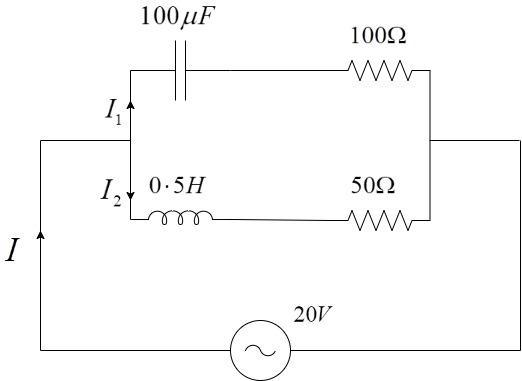
A) The current through the circuit, I is 0.3A
B) The current through the circuit, I is

Answer
490.5k+ views
Hint:If there was a DC source, we could have directly considered the parallel combination of resistors and calculated the net current from the total resistance. As there is an AC source, along with the resistances, we have to also, account for the reactances offered by the inductor and the capacitor, while calculating the branch currents across the branches.
Also, we cannot directly add the impedances as we do in parallel circuits, since the values will be in different phases. So, we have to draw a phasor diagram to solve for the net impedance and hence, the net current in the circuit.
Complete step by step solution:
We have to calculate the individual currents in the branches.
The impedance is the obstruction offered to the flow of A.C current in the circuit.
To find the net impedance in the circuit, we have to individually calculate the impedance of the top branch and then, the individual currents and then, we can add the phasors.
Impedance in the lower branch,
Given the angular frequency,
Inductance,
Resistance in the lower branch,
Substituting, we get –
The direction,
Current through the lower branch,
Similarly,
Impedance in the upper branch,
Given the angular frequency,
Capacitance,
Resistance in the upper branch,
Substituting, we get –
The direction,
Current through the upper branch,
Therefore, the current in the upper branch is
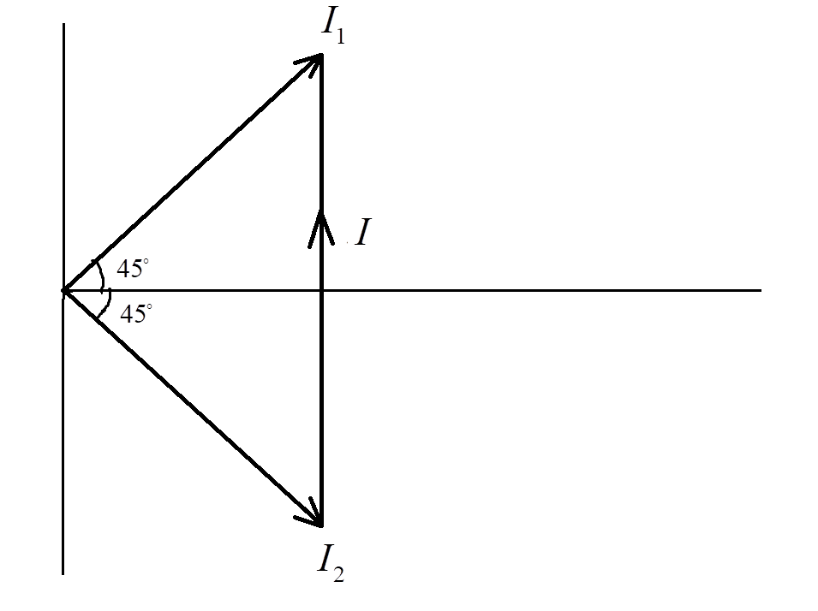
From the phasor, the net current I, is the vector sum of the individual currents. From the above figure, we get –
Magnitude of I,
Thus,
The net current in the circuit,
Voltage across the
Voltage across the
Thus, Statement-A and Statement-C are the only correct statements in the above question.
The correct options are Option A and Option C.
Note:While solving the problem, the students should always note the direction of the current and the relationship between the voltage and current in the phasor diagram.
Note that the current
Complete step by step solution:
We have to calculate the individual currents in the branches.
The impedance is the obstruction offered to the flow of A.C current in the circuit.
To find the net impedance in the circuit, we have to individually calculate the impedance of the top branch and then, the individual currents and then, we can add the phasors.
Impedance in the lower branch,
Given the angular frequency,
Inductance,
Resistance in the lower branch,
Substituting, we get –
The direction,
Current through the lower branch,
Similarly,
Impedance in the upper branch,
Given the angular frequency,
Capacitance,
Resistance in the upper branch,
Substituting, we get –
The direction,
Current through the upper branch,
Therefore, the current in the upper branch is

From the phasor, the net current I, is the vector sum of the individual currents. From the above figure, we get –
Magnitude of I,
Thus,
The net current in the circuit,
Voltage across the
Voltage across the
Thus, Statement-A and Statement-C are the only correct statements in the above question.
The correct options are Option A and Option C.
Note:While solving the problem, the students should always note the direction of the current and the relationship between the voltage and current in the phasor diagram.
Note that the current
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




