Question

In the given diagram, PQU is an equilateral triangle, QRVU is a square and RSTU is a parallelogram. Find the perimeter, (in cm) of the whole diagram.
 A) \[26 + 4\sqrt 2 \]
 B) \[21\]
C) \[26 + 8\sqrt 2 \]
D) \[25 + 8\sqrt 2 \]

Answer 1

Hint: Perimeter is the sum of all the sides of the figure. Hence we have to add all the sides of the given figure to get the desired answer. Here in this question we need to find the length of all the sides and add them all to get the perimeter.

Complete step-by-step answer:

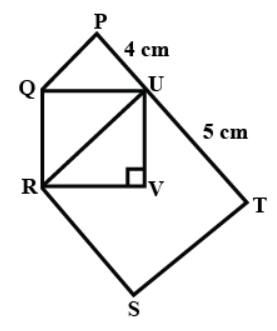
Since the triangle PQU is an equilateral triangle
Therefore, all the sides of the triangle are equal.
\[PQ = PU = QU = 4\;cm\]
Now since QRVU is a square and all the sides of the square are equal
Therefore,
\[QU = UV = VR = QR = 4\;cm\]
Now, since RSTU is a parallelogram and the opposite sides of the parallelogram are equal therefore,
\[\;UT = SR = 5\;cm\]
Also,
\[RU = ST\]………………………….(1)
Now since RU is the diagonal of the square QRVU therefore we have to first calculate the diagonal
The diagonal of the square is given by:
\[{\text{diagonal}} = \sqrt 2 \times {\text{side}}\]
Putting in the values we get:-
\[
  RU = \sqrt 2 \times \left( 4 \right) \\
  RU = 4\sqrt 2 cm \\
 \]
Putting this value in equation 1 we get:-
\[RU = ST = 4\sqrt 2 cm\]
Now since the perimeter of any figure is the sum of all sides of the figure
Hence the perimeter of the given figure is:-
\[
  Perimeter = PU + UT + TS + SR + QR + PQ \\
  Perimeter = (4 + 4 + 5 + 5 + 4 + 4 + 4\sqrt 2 + 4\sqrt 2 )cm \\
  Perimeter = 26 + 8\sqrt {2} \;cm. \\
 \]
Hence the perimeter of the given figure is \[26 + 8\sqrt {2} \;cm\]
Therefore, option (d) is the correct option.

Note: The sides of the equilateral triangle are equal.
All the sides of the square are equal.
The opposite sides of a parallelogram are equal.
The diagonal of a square is given by:-
\[{\text{diagonal}} = \sqrt 2 \times {\text{side}}\]
The diagonal can also be calculated by using Pythagora's theorem of triangles.
The Pythagoras formula is given by:-
\[{\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^{\text{2}}}{\text{ + }}{\left( {{\text{perpendicular}}} \right)^2}\]