Question

In the given figure ABC is a triangle and D is midpoint of BC. AD is produced to E. BM and CN are perpendiculars dropped from B and C respectively on AE.
Prove that:
1.\[\vartriangle BMD \cong \vartriangle CND\]
2.\[BM = CN\]

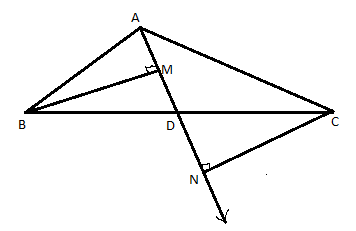
Answer 1

Hint: In order to prove the triangles are congruent we have to use any of the tests of congruency. With the help of that we can prove statement 1 and will automatically prove statement 2.

Complete step-by-step answer:
Given that in figure D is the midpoint of BC.

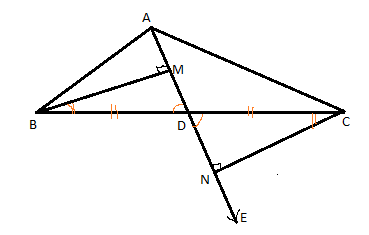
Observe the figure redrawn,
Now, consider \[\vartriangle BMD\] and \[\vartriangle CND\]
\[BD = CD \to \] D is the midpoint of BC.
\[\angle BDM = \angle CDN \to \] Vertically opposite angles
\[\angle MBD = \angle NDC \to \] alternate angles
So the two triangles are congruent by ASA test.
\[\vartriangle BMD \cong \vartriangle CND\]
Hence proved the first statement.
So now triangles are congruent ,
\[BM = CN\] \[ \to \vartriangle BMD \cong \vartriangle CND\]
Hence proved the second statement.
Note: Remember D is midpoint of BC is the key point to prove the triangles are congruent. Check which congruency test we can use to show triangles are congruent. Here two angles of right angle measurements are given but their included side DM and ND have no condition of equality.