Question

In the given figure, ABCD is a parallelogram; E and F are the midpoints of sides AB and CD respectively. Prove that, the line segments AF and CE trisect the diagonal BD.

Answer 1

Hint: We have given a parallelogram ABCD with diagonal BD and two line segments AF and CE so we have to show that AF and CE trisect the diagonal BD meaning we have to first of all show that $DP=PQ=QB$ and then let us assume that all the three line segments are equal to some constant say x and addition of all the three line segments are equal to BD so three times x is equal to BD and we get x as one-third of BD. To show $DP=PQ=QB$, we have to show $FC=AE$ and AF parallel to CE. Then take the triangle DQC and it is already given that F is the midpoint of the line segment CD and we have proved that PF is parallel to QC so from the theorem which says that if a line is drawn midpoint of the one side of the triangle and parallel to another side will bisect the third side $DP=PQ$. Similarly, taking triangle APB we can show that $PQ=QB$. Combining the result of $DP=PQ$ and $PQ=QB$ we can say $DP=PQ=QB$.

Complete step-by-step solution:
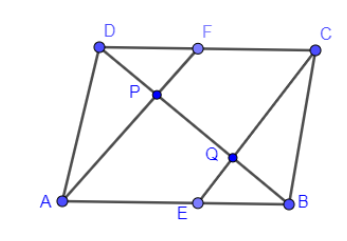
We have given a parallelogram which is drawn below, in which E and F are midpoints of sides AB and CD and a diagonal BD is also drawn.

We have to show that line segments AF and CE bisects the diagonal BD. So, to prove that we are going to show $DP=PQ=QB$.
It is given that ABCD is a parallelogram meaning $AB=CD$ and AB is parallel to CD also.
As AB is parallel to CD so we can say that AE is parallel to CF. The reason behind AE parallel to CF is that line segments AE and CF are the parts of the parallel line segments AB and CD and we know that parts of parallel line segments are also parallel.
Now, $AB=CD$ taking half on both the sides we get,
$\dfrac{1}{2}AB=\dfrac{1}{2}CD$
It is given that E and F are midpoints of sides AB and CD so we can write half of AB as AE and half of CD as CF.
$AE=CF$

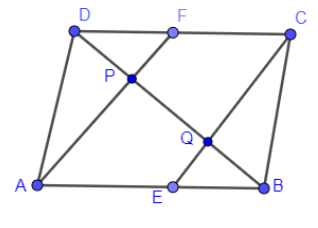
Now, if you look in AECF, we have shown the following things:
$\begin{align}
  & AE\parallel CF \\
 & AE=CF \\
\end{align}$
As we have shown the one pair of opposite sides are parallel and equal so we can say that AECF is a parallelogram.
Hence, AECF is a parallelogram. Now, if AECF is a parallelogram then AF is parallel to CE and if AF is parallel to CE then PF is also parallel to QC.
Now, we are going to consider the triangle DQC. In the below diagram, we have snipped the triangle DQC from the parallelogram ABCD for better understanding.

In this triangle, we have shown the following things in the above:
$PF\parallel QC$
And F is the midpoint of DC so $DF=FC$.
Now, considering the above two properties of triangle DQC there is a theorem which states that if a line is drawn midpoint of the one side of the triangle and parallel to another side will bisect the third side so using this theorem we can say that point P bisects DQ.
$DP=PQ$
Now, we got one of the equations written in the required equation $DP=PQ=QB$.
Similarly, we can take triangle APB and will prove that $PQ=QB$. The proof is exactly in the same way that we have done for triangle DQC.
Hence, we got the two equalities:
$\begin{align}
  & DP=PQ \\
 & PQ=QB \\
\end{align}$
From the above two equalities, we can write $DP=PQ=QB$.
Now, let us assume that $DP=PQ=QB$ is equal to some constant say x then:
$DP=PQ=QB=x$
And from the figure, the sum of DP, PQ, and QB is equal to BD.
$DP+PQ+QB=DB$
Substituting $DP=PQ=QB=x$ in the above equation we get,
$\begin{align}
  & x+x+x=DB \\
 & \Rightarrow 3x=DB \\
 & \Rightarrow x=\dfrac{DB}{3} \\
\end{align}$
Hence, we have shown that the segments DP, PQ, and QB are having a length of one-third of the diagonal BD. In other words, we have shown that line segments AF and CE are trisecting the diagonal BD.

Note: The most common thing, which we take for granted if you see the figure given in the above problem. We have redrawn the figure below for better understanding.

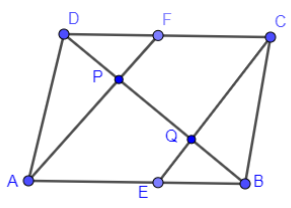
Now, if you see the above figure, you might think that AF is parallel to EC and you forget to prove them. So, beware of making this blunder. You have to prove AF is parallel to EC just because it is looking parallel; we cannot assume them as parallel. Then you might say that we have also written AB is parallel to CD in the above solution because it is given in the question in the statement form that ABCD is a parallelogram.