Question

In the given figure, ABCD is a rectangle of dimensions $21cm\times 14cm$. A semicircle is drawn with BC as diameter. Find the area and the perimeter of the shaded region in the below figure.

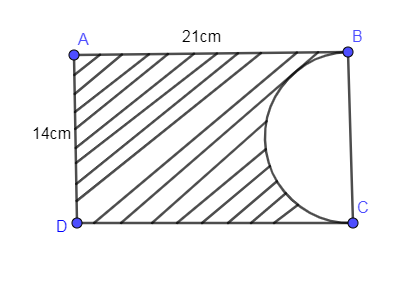
Answer 1

Hint: To find the area of the shaded region, we are going to find the area of the rectangle ABCD first then we are going to find the area of the semi-circle. After that, we are going to subtract the area of the semicircle from the area of the rectangle ABCD. We know that the area of the rectangle is equal to the multiplication of length and breadth. And the area of the semicircle is equal to half of the area of a circle. The perimeter of the shaded figure is the addition of two opposite lengths with the breadth of the rectangle and in this addition, we are going to add the perimeter of the semi-circle.

Complete step-by-step solution:
The figure given in the problem is as follows:

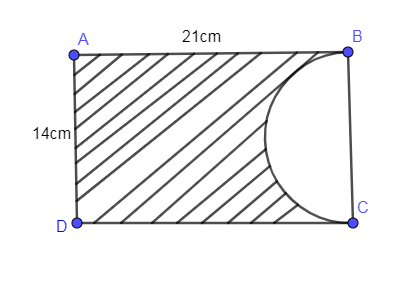
Now, we are going to find the area of the rectangle ABCD first. We know that the area of the rectangle is equal to the multiplication of length and breadth. The length given in the above figure is equal to 21cm and the breadth given in the above problem is equal to 14 cm so multiplying both the length and the breadth we get the area of the rectangle as follows:
$\begin{align}
  & \Rightarrow 21cm\times 14cm \\
 & =294c{{m}^{2}} \\
\end{align}$
From the above, we have found the area of the rectangle as $294c{{m}^{2}}$.
Now, we are going to find the area of the semi-circle. We know that the area of the semi-circle is equal to half of the area of the circle.
Let us say, we have a circle with radius “r” then the area of the circle is equal to:
$\pi {{r}^{2}}$
Half of the above area is equal to:
$\dfrac{1}{2}\pi {{r}^{2}}$
The length of the side BC is 14cm which is the diameter of the semi-circle then the radius of the semi-circle is equal to half of this diameter so the radius of the semi-circle is equal to:
$\begin{align}
  & \dfrac{14}{2}cm \\
 & =7cm \\
\end{align}$
Now, we are going to find the area of the semi-circle as follows:
$\begin{align}
  & \dfrac{1}{2}\left( \dfrac{22}{7} \right){{\left( 7cm \right)}^{2}} \\
 & =11\times 7c{{m}^{2}} \\
 & =77c{{m}^{2}} \\
\end{align}$
Subtracting the area of the semicircle from the area of the rectangle we will get the area of the shaded region,
$\begin{align}
  & 294c{{m}^{2}}-77c{{m}^{2}} \\
 & =217c{{m}^{2}} \\
\end{align}$
From the above, we got the area of the shaded region as $217c{{m}^{2}}$.
Now, we are going to find the perimeter of the shaded region which we are going to find by adding lengths AB, AD and DC and we get,
$\begin{align}
  & AB+AD+DC=21cm+14cm+21cm \\
 & \Rightarrow AB+AD+DC=56cm..........(1) \\
\end{align}$
And in the above summation, we are going to add the circumference of the semi-circle.
We know that the circumference of a semicircle is equal to half of the circumference of a circle.
Let us take the circle with radius “r” then the formula for the circumference of the circle is equal to:
$2\pi r$
Half of the above circumference is equal to:
$\dfrac{2\pi r}{2}=\pi r$
Substituting “r” as 7cm in the above formula we get,
$\begin{align}
  & \dfrac{22}{7}\times 7cm \\
 & =22cm \\
\end{align}$
Now, adding the above circumference of semi-circle to eq. (1) we get,
$\begin{align}
  & 56cm+22cm \\
 & =78cm \\
\end{align}$
From the above, we have found the perimeter of the shaded region as 78cm.
Hence, we have found the area and perimeter of the shaded region as $217c{{m}^{2}}$ and 78cm respectively.

Note: To solve the above problem, you must have knowledge of how to find the area of the rectangle, area of the semi-circle. And also you should know what a perimeter and area mean. Along with that, you must know what the formula for the circumference of the semicircle is.