Question

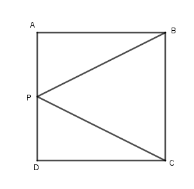
In the given figure, ABCD is a square and P is the midpoint of AD. BP and CP are joined. Prove that ∠PCB = ∠PBC.

Answer 1

Hint: Here, consider triangles PBA and PCD and check whether they are congruent or not. Apply CPCT to equate ∠ABP and ∠PCD. As we know all angles of a square is 90°. Therefore, ∠ DCB = ∠ ABC = 90°. From 90° subtract ∠DCP and ∠ABP to get ∠PBC and ∠PCB.

Complete step-by-step answer:
 In the given figure, ABCD is a square and P is the midpoint of AD. That is AB = BC = CD = AD and AP = PD.
 In triangle PBA and PCD,
PA = PD (P is the midpoint of AD)
∠ PAB = ∠ PDC (Each = 90°)
AB = DC (Sides of a square)
So, $ \vartriangle PBA \cong \vartriangle PCD $
 $ \Rightarrow $ ∠ ABP = ∠ PCD (By CPCT)
Now, if equals are subtracted from equals then the result is also equal.
∠ ABP + ∠ PBC = ∠ PCD + ∠ PCB
∠ PBC = ∠ PCB (∠ ABP and ∠ PCD canceled out as they are equal)

Note: In these types of questions, first use the properties the properties i.e., all sides of a square are equal and all angles of a square are equal to 90°. In this question we have used the concept of congruent triangles and CPCT. CPCT means corresponding parts of congruent triangles i.e., if two triangles are congruent, then each side and each angle of one triangle are equal to the side and angle of another triangle.
Alternatively, in triangle BPC
PB = PC
∠ PBC = ∠ PCB (Angles opposite to equal sides are equal)