Question

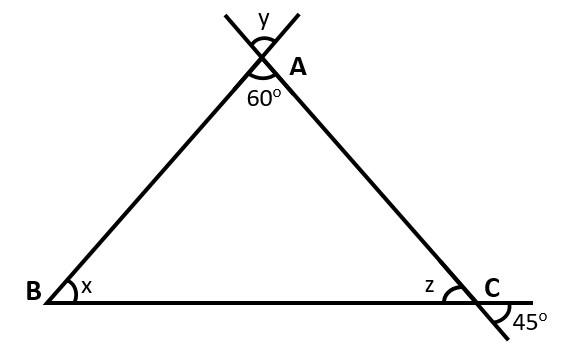
In the given figure find the value of $x$ and $y$.

Answer 1

Hint: Here, we should apply the property that vertically opposite angles are equal. By this property, find $y$ and z. Also apply the theorem that the sum of the angles of a triangle is ${{180}^{\circ }}$. With the help of this theorem, find the value of $x$.

Complete step-by-step answer:
We are given a figure. With the help of figures we have to find the value of $x$ and $y$.
First, let us find the value of $y$.
We know by a property that vertically opposite angles are equal.
Here, $y$ and $\angle BAC$ are vertically opposite angles. Therefore, we can say that
$y=\angle BAC$
In the figure, $\angle BAC={{60}^{\circ }}$. Hence, we will get $y={{60}^{\circ }}$.
Now, we have to find the value of $x$, for that first we have to find the value of $z$.
Again, by the property that vertically opposite angles are equal, as from the figure we can say that
 $z={{45}^{\circ }}$.
Next, to find the value of $x$, consider the triangle $\vartriangle ABC$.
We know that the sum of all the three angles of a triangle is ${{180}^{\circ }}$.
Therefore, in $\vartriangle ABC$ we have,
$x+z+\angle BAC={{180}^{\circ }}$
We know that $\angle BAC={{60}^{\circ }}$and $z={{45}^{\circ }}$.
Therefore, our equation becomes:
$\begin{align}
  & x+{{45}^{\circ }}+{{60}^{\circ }}={{180}^{\circ }} \\
 & x+{{105}^{\circ }}={{180}^{\circ }} \\
\end{align}$
In the next step by taking ${{105}^{\circ }}$to the right side, it becomes$-{{105}^{\circ }}$. Therefore we get:
$\begin{align}
  & x={{180}^{\circ }}-{{105}^{\circ }} \\
 & x={{75}^{\circ }} \\
\end{align}$

Note: After getting the answer check whether you are getting the sum of all angles of the triangle as ${{180}^{\circ }}$. If you are not getting ${{180}^{\circ }}$ then probably your answer would be wrong. Here, first you have to apply the property that vertically opposite angles are equal to find $z$ otherwise you won’t get the value of $x$.