Question

In the given figure, the arms of two angles are parallel. If $\angle ABC={{70}^{\circ }}$ , then find:
i)$\angle DGC$
ii)$\angle DEF$

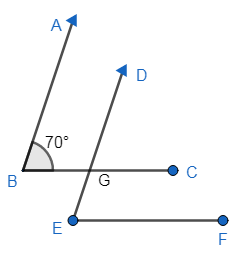
Answer 1

Hint: At first use the concept of parallel and property that corresponding angles are equal to say to $\angle ABC=\angle DGC$ and then apply the same property to say $\angle DGC=GEF$ or $\angle ABC=\angle GEF$. Then find the given values by the given data.

Complete step-by-step answer:
In this question we are given a figure and the value of $\angle ABC$as ${{70}^{\circ }}$ . So, from the given data we have to find a measure of angles $\angle DGC$ and $\angle DEF$ .
So, at first we will draw the figure given ,

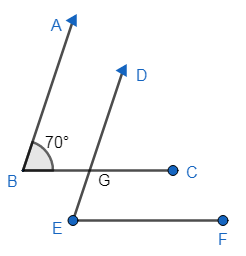
Now before proceeding let’s learn something about angles,
Angles formed by two lines in a plane, but this plane does not have to be a Euclidean plane. Angles formed by the intersection of two curves in a plane are defined as the angles determined by the tangent rays at the point of intersection. Angles are also formed by the intersection in Euclidean and other spaces. These are called dihedral angles. Angles are used to designate the measure of an angle or of rotation. In plane geometry an angle is formed by two rays, called the sides of a triangle sharing a common endpoint called vertex of angle. In case of rotation, the arc is centered at the centre of the rotation and delineated by any other point and its image by the rotation.
There also some properties of parallel lines like of two lines let’s say AB and CD is parallel and a transversal is cut by a line let’s say XY as represented below,

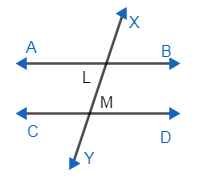
Let's say points of intersection are L, M so according to the properties $\angle XLB=\angle LMD,\angle MLB=\angle YMD,\angle XLA=\angle LMC,\angle ALM=\angle CMY$ as corresponding angles are equal.
Also along with them $\angle LB=\angle LMC,\angle ALM=\angle LMD$ as alternate angles are equal.

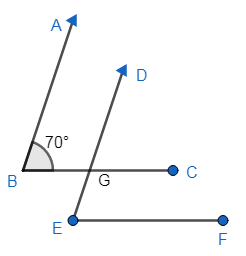
Now, in the given question by using properties of parallel lines we can say that $\angle ABC=\angle DGC$ as corresponding angles are equal because AB is parallel to DG.
Then we can say that $\angle DGC=\angle DEF$ as corresponding angles are equal because BC is parallel to EF. So we can say $\angle ABC=\angle DEF$ .
Now as we know $\angle ABC={{70}^{\circ }}$ as it was given so $\angle DGC$ is ${{70}^{\circ }}$ and $\angle DEF$ is also ${{70}^{\circ }}$.

Hence the value of $\angle DGC$ is ${{70}^{\circ }}$and the value of $\angle DEF$is ${{70}^{\circ }}$.

Note: We can find angle DEF in another way. We know that $\angle ABC=\angle BGE$ as alternate angles are equal as AB and DE is parallel. Then we can say that $\angle BGE=\angle GEF$ as alternate angles are equal as BC and EF is parallel.