Question

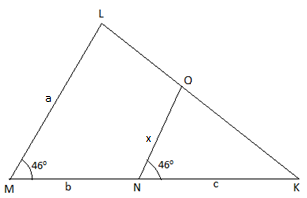
In the given figure, x equals:

A. \[\dfrac{ab}{a+c}\]
B. \[\dfrac{ac}{a+b}\]
C. \[\dfrac{ac}{b+c}\]
D. \[\dfrac{ab}{b+c}\]

Answer 1

Hint: In the above question, we will use the concept of similarity of two triangles. We can observe that LM is parallel to ON so the triangle KLM and the triangle KON is similar by AA similarity criterion. Then we will use the properties that corresponding sides of similar triangles are in proportion.

Complete step-by-step answer:
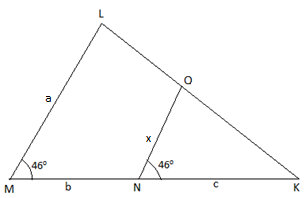
We have been given the figure as below:

It is given that \[\angle LMK=\angle ONK={{46}^{\circ }}\]
We know that this is the corresponding angle which is possible only if ON is parallel to LM.
Hence, ON is parallel to LM.
\[\Rightarrow \angle MLO=\angle NOK\]
Since ON is parallel to LM, this is a corresponding angle.
Now in \[\Delta LMK\] AND \[\Delta ONK\], we have,
\[\angle LMC=\angle ONK={{46}^{\circ }}\], which is given.
\[\angle MLO=\angle NOK\]
Since LM is parallel to ON and this is the corresponding angle.
\[\Rightarrow \Delta LMK\sim \Delta ONK\] by AA similarity.
We know that if two triangles are similar to each other then their sides are in proportion.
\[\Rightarrow \dfrac{LM}{ON}=\dfrac{MK}{NK}\]
We have been given LM = a, MK = MN + NK = b + c, ON = x and NK = c.
So by substituting these values in the above expression, we get as follows:
\[\dfrac{a}{x}=\dfrac{b+c}{c}\]
On cross multiplication, we get as follows:
\[ac=x(b+c)\]
On dividing the equation by (b + c) we get as follows:
\[\begin{align}
  & \dfrac{ac}{b+c}=\dfrac{x(b+c)}{(b+c)} \\
 & \Rightarrow \dfrac{ac}{b+c}=x \\
\end{align}\]
Therefore, the correct answer of the above question is option C.

Note: Be careful while choosing the option as all the options look quite similar. Also be careful while substituting the values in the proportion. Remember that if two triangles are similar, then their corresponding sides are in proportion.