Question

In the given graph. The slope of line of AB gives the information of the.

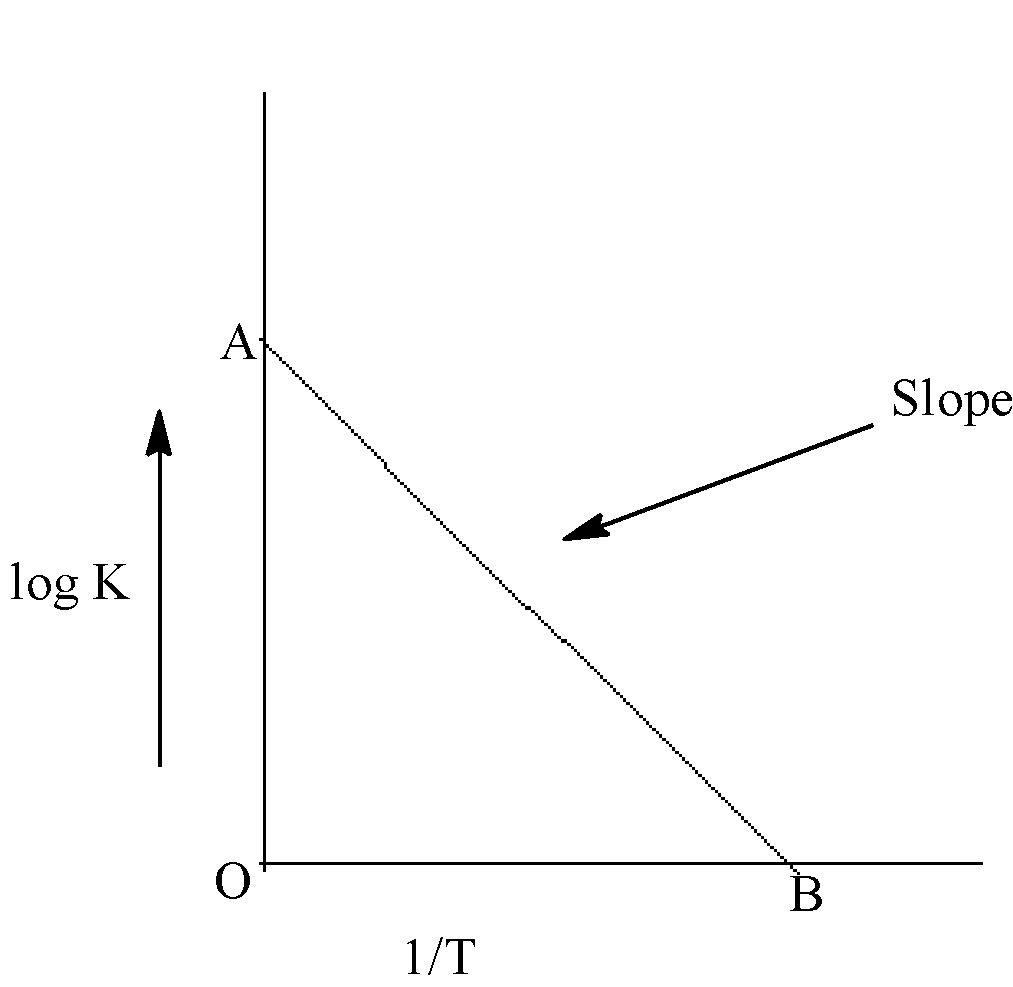
A) Value of $\dfrac{{{E_a}}}{{2.303}}$
B) Value of $\dfrac{{2.303}}{{{E_a}}}$
C) Value of $ - \dfrac{{{E_a}}}{{2.303R}}$
D) Value of $ - \dfrac{{{E_a}}}{{2.303RT}}$

Answer 1

Hint: We Know the Arrhenius equation,
The Arrhenius equation is $K = A{e^{ - Ea/RT}}$
The rate constant of the reaction is K.
The activation energy of the reaction is ${E_a}$
R is the gas constant of the reaction
We must remember that the frequency factor or Arrhenius factor explains the rate of collision and the fraction of collisions with the proper orientation for the reaction to occur and it is denoted as

Complete step by step answer:
Now we take the natural logarithm on both sides of Arrhenius equation we get,
\[ \Rightarrow lnk = lnA - Ea/RT\]
Thus, ${\log _{10}}K = \log A - \dfrac{{{E_a}}}{{2.303T}}$

So, the correct answer is Option C .

Note:
Let us discuss the concept of activation energy.
The difference between the energy state of reactants and therefore the transition state for the reaction to happen reactants got to cross the transition state energy barrier and hence lower energy of activation faster is going to be the reaction.
One can calculate the activation energy if two known temperatures are directly given and a rate constant at each temperature is known using the equation.
$\log \,\dfrac{{{K_2}}}{{{K_1}}} = - \dfrac{{{E_a}}}{{2.303\,R}}\left[ {\dfrac{{{T_1} - {T_2}}}{{{T_1}{T_2}}}} \right]$
Where \[{T_{1{\text{ }}}}and{\text{ }}{T_2}\] two different temperatures, \[{k_1}{\text{ }}and{\text{ }}{k_2}\] are reaction rate constants.
Example:
The activation energy of a reaction when its rate is double if the temperature is raised from ${20^ \circ }C - {35^ \circ }C$ can be calculated as,
Hence the rate of the reaction is doubled on raising the temperature, thus the rate of the reaction is,
${r_2} = 2{r_1}$
We know that the rate of the reactions and the reactions rate are proportional to each other,
$\dfrac{{{K_2}}}{{{K_1}}} = 2$
Substituting the know values in the equation,
$\log \,2 = - \dfrac{{{E_a}}}{{2.303\,\left( {8.314} \right)}}\left[ {\dfrac{{{{293}_1} - 308}}{{293 \times 308}}} \right]$
$0.3010 = - \dfrac{{{E_a}}}{{2.303\,\left( {8.314} \right)}}\left[ {\dfrac{{ - 15}}{{293 \times 308}}} \right]$
${E_a} = \dfrac{{0.3010 \times 2.303 \times 8.314 \times 293 \times 308}}{{15}}$
On simplifying we get,
${E_a} = 34.67kJmo{l^{ - 1}}$
The activation energy for a reaction is $34.67kJmo{l^{ - 1}}$.