
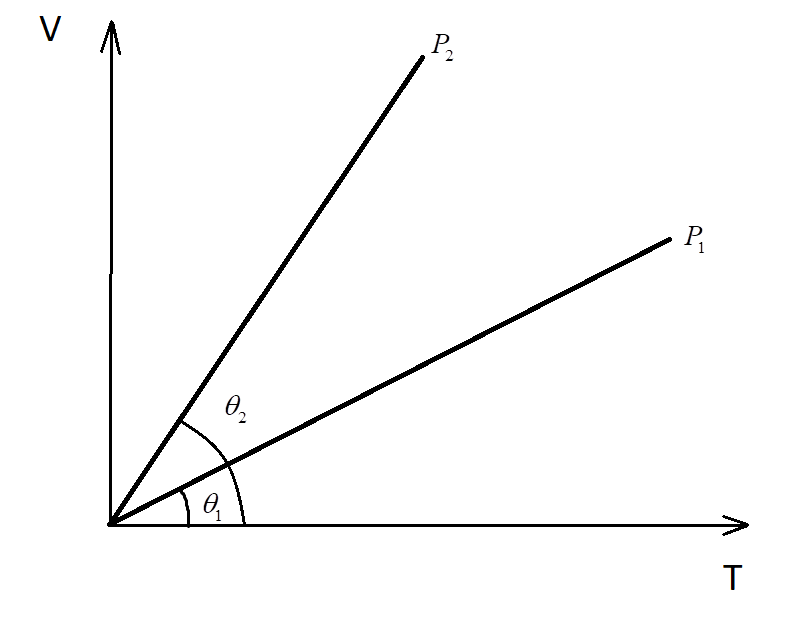
In the given (V-T) diagram, what is the relation between pressures ${P_1}$ and ${P_2}$?

Answer
531.3k+ views
Hint: The linear curve is passing through origin in volume (V) versus temperature (T) suggests that the given thermodynamic process is isobaric. In the isobaric process, the pressure of the thermodynamic system remains constant. To get the required relationship between the pressures for the given curves we will compare the slope of each curve and use the relation: slope $ = \left( {\dfrac{{nR}}{P}} \right)$, where n is the number of moles, R is the universal gas constant and P is the pressure.
Complete answer:
Consider the volume-temperature graph with two lines at different pressures ${P_1}$ and ${P_2}$.
Step I: Establish the relation between volume
An isobaric process is a constant pressure process. i.e., in an isobaric process, we have
$P = $Constant…………. (i)
By using ideal gas law:
$PV = nRT$
$ \Rightarrow \dfrac{V}{T} = \dfrac{{nR}}{P}$………………….. (ii)
Using equation (i) in (ii), we get
$ \Rightarrow \dfrac{V}{T} = $Constant
$ \Rightarrow V = CT$…………………… (iii), where C is a constant which is equal to $\left( {\dfrac{{nR}}{P}} \right)$.
∴ $V \propto T$
From equation (ii) we can say that the V-T graph is a straight line passing through the origin.
Step II: Calculate the slope of the isobaric curve.
From equation (ii)
$V = \dfrac{{nRT}}{P}$……. (iv)
Differentiating equation (iv) with respect to T.
$\dfrac{{dV}}{{dT}} = \dfrac{{nR}}{P} = $Slope
i.e., Slope$ \propto \dfrac{1}{P}$
So, if the slope of the curve increases then the pressure will decrease and vice versa.
Since from the given V-T graph:
${\theta _2} > {\theta _1}$
$ \Rightarrow $The slope of curve 2 > Slope of curve 1
$ \Rightarrow {P_2} < {P_1}$
Hence, the pressure of the second is lesser than the pressure in the first curve.
Note:
Students should note that in the isobaric process the pressure will remain constant and the V-T graph for the process is a straight line passing through the origin. While in the case of the P-V graph it will be horizontal and parallel to the volume axis.
Complete answer:
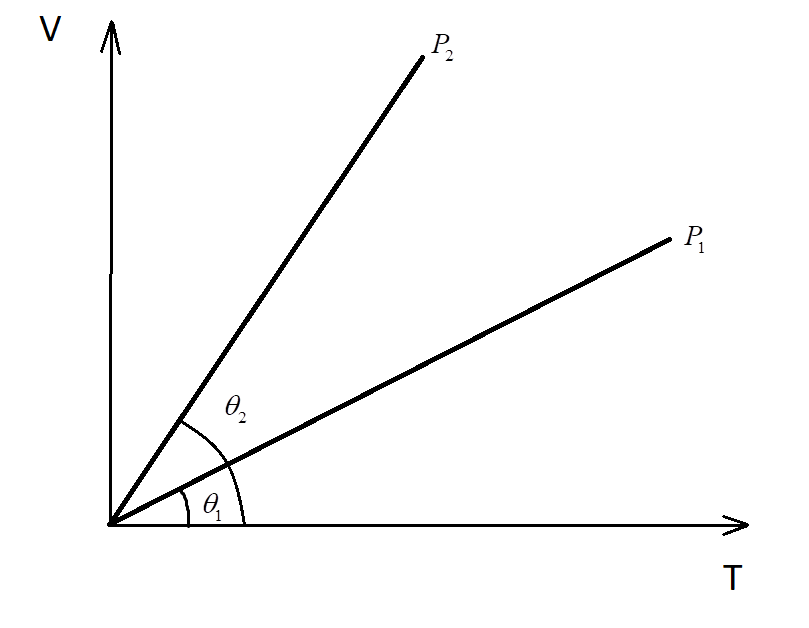
Consider the volume-temperature graph with two lines at different pressures ${P_1}$ and ${P_2}$.

Step I: Establish the relation between volume
An isobaric process is a constant pressure process. i.e., in an isobaric process, we have
$P = $Constant…………. (i)
By using ideal gas law:
$PV = nRT$
$ \Rightarrow \dfrac{V}{T} = \dfrac{{nR}}{P}$………………….. (ii)
Using equation (i) in (ii), we get
$ \Rightarrow \dfrac{V}{T} = $Constant
$ \Rightarrow V = CT$…………………… (iii), where C is a constant which is equal to $\left( {\dfrac{{nR}}{P}} \right)$.
∴ $V \propto T$
From equation (ii) we can say that the V-T graph is a straight line passing through the origin.
Step II: Calculate the slope of the isobaric curve.
From equation (ii)
$V = \dfrac{{nRT}}{P}$……. (iv)
Differentiating equation (iv) with respect to T.
$\dfrac{{dV}}{{dT}} = \dfrac{{nR}}{P} = $Slope
i.e., Slope$ \propto \dfrac{1}{P}$
So, if the slope of the curve increases then the pressure will decrease and vice versa.
Since from the given V-T graph:
${\theta _2} > {\theta _1}$
$ \Rightarrow $The slope of curve 2 > Slope of curve 1
$ \Rightarrow {P_2} < {P_1}$
Hence, the pressure of the second is lesser than the pressure in the first curve.
Note:
Students should note that in the isobaric process the pressure will remain constant and the V-T graph for the process is a straight line passing through the origin. While in the case of the P-V graph it will be horizontal and parallel to the volume axis.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is a periderm How does periderm formation take class 11 biology CBSE




